




Next: Some practical considerations
Up: Mallia-Zarb: Kirchhoff migration
Previous: THEORETICAL APPROACH
In practice, 2-D Kirchhoff migration is carried out by summing the
amplitudes in (x,t) space along the diffraction curve that corresponds to
Huygen's secondary source at each point in (x,z) space. For
zero-offset
sections, the moveout at a source-receiver point a distance x from the
apex of a diffraction hyperbola at time t0 is given by:
| 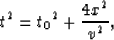 |
(2) |
while for common-offset sections, the moveout is given by:
| ![\begin{displaymath}
t={\left[\frac{{(x+s/2)}^2}{v^2}
+\frac{{t_0}^2}{4} \right]}...
...ft[ \frac{{(x-s/2)}^2}{v^2}
+\frac{{t_0}^2}{4} \right]}^{1/2},\end{displaymath}](img8.gif) |
(3) |
where s is the value of offset and v is the velocity at
the apex of the hyperbola.
Before summation, each sample is scaled by the obliquity factor,
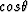 , and the spherical spreading factor (1/vt)1/2.
After summation the output section is convolved with a filter
whose amplitude-frequency response is proportional to the square
root of frequency, with a constant phase delay of
, and the spherical spreading factor (1/vt)1/2.
After summation the output section is convolved with a filter
whose amplitude-frequency response is proportional to the square
root of frequency, with a constant phase delay of 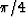 . The latter
corresponds to the half-derivative that was mentioned earlier on.
. The latter
corresponds to the half-derivative that was mentioned earlier on.





Next: Some practical considerations
Up: Mallia-Zarb: Kirchhoff migration
Previous: THEORETICAL APPROACH
Stanford Exploration Project
11/11/1997
![\begin{displaymath}
t={\left[\frac{{(x+s/2)}^2}{v^2}
+\frac{{t_0}^2}{4} \right]}...
...ft[ \frac{{(x-s/2)}^2}{v^2}
+\frac{{t_0}^2}{4} \right]}^{1/2},\end{displaymath}](img8.gif)
![]() , and the spherical spreading factor (1/vt)1/2.
After summation the output section is convolved with a filter
whose amplitude-frequency response is proportional to the square
root of frequency, with a constant phase delay of
, and the spherical spreading factor (1/vt)1/2.
After summation the output section is convolved with a filter
whose amplitude-frequency response is proportional to the square
root of frequency, with a constant phase delay of ![]() . The latter
corresponds to the half-derivative that was mentioned earlier on.
. The latter
corresponds to the half-derivative that was mentioned earlier on.