Constant velocity sections

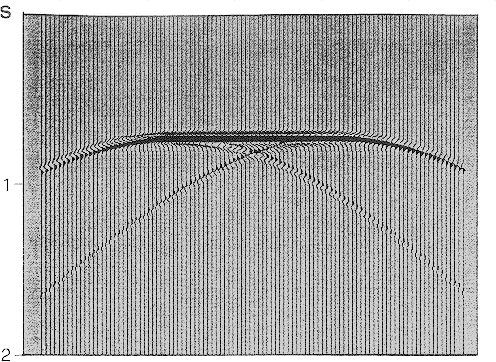
Figure 1 shows a simple flat horizon as a reflection profile on a depth section converted to two-way traveltime. Figures 2 and 3 show, respectively, the zero-offset and common-offset seismic response of the reflector. In generating the seismic response in Figure 3, the common offset distance was taken as 1000 m. The reflector is assumed to lie in a medium of constant velocity equal to 2000 m/s.

 

f3-8a
Figure 1 Horizontal reflector (constant velocity, 2000 m/s).

 

f3-8b
Figure 2 Zero-offset seismic response of horizontal reflector model.

 

f3-18a
Figure 3 Common-offset seismic response of the horizontal reflector model.

The zero-offset response shows that the reflected horizon remains unshifted in time. However the edges give rise to diffracted energy, and the ends of the reflector are now not so clearly defined. Figure 4 shows that migration successfully collapses the diffractions, and the edges of the horizon are once more shown to lie at their true lateral positions.

 

f3-8c
Figure 4 Migration of zero-offset section.

 

f3-18b
Figure 5 Migration of common-offset section.

Referring to the common-offset seismic response in Figure 3 and comparing this section to the zero-offset response in Figure 2, the whole reflector is shifted down the section by a time interval which is determined by the source-receiver separation. It is also evident that seismic diffractions in nonzero-offset records behave in a similar way to those shown on zero-offset sections. Figure 5 shows the output migrated image. All points on the reflector have been correctly repositioned in time and space. Diffracted energy has been completely removed, and the lateral termination points of the horizon have been redefined accurately.