In the spatial and frequency domain, the 3-D acoustic wave equation can be formulated as
| (1) |
where ![]() can be approximated by the
WKBJ Green's function
can be approximated by the
WKBJ Green's function
| (2) |
where ![]() is the traveltime from source
is the traveltime from source
![]() to an arbitrary point
to an arbitrary point ![]() . Using the WKBJ Green's function,
Beylkin 1985 gave an inversion formula in 3-D media
. Using the WKBJ Green's function,
Beylkin 1985 gave an inversion formula in 3-D media
| (3) |
In the above formula, ![]() is the perturbation
to the background velocity
is the perturbation
to the background velocity ![]() . The updated velocity model is
given by
. The updated velocity model is
given by
| (4) |
S0 is the 2-D integral surface.
![]() is introduced by Beylkin 1985, which is
associated with the ray curvature.
is introduced by Beylkin 1985, which is
associated with the ray curvature.
![]() and
and ![]() are the WKBJ Green's
function.
are the WKBJ Green's
function. ![]() is a high-pass filter determined the source.
is a high-pass filter determined the source.
![]() represents the observed data at
represents the observed data at ![]() due to the source
due to the source
![]() .
.
Bleistein et al.1987 specialize the 3-D formula to the 2.5-D geometry using the method of stationary phase. The corresponding 2.5-D inversion formula is
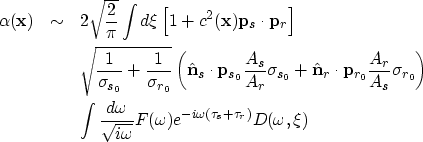 |
||
| (5) |
Here, ![]() and
and ![]() are the slowness vectors at the
imaging location pointing to the source and receiver respectively.
are the slowness vectors at the
imaging location pointing to the source and receiver respectively.
![]() and
and ![]() are the parameters defined by the following
equations
are the parameters defined by the following
equations
| (6) |
![]() and
and ![]() are unit downward normals at the
source and receiver points respectively.
are unit downward normals at the
source and receiver points respectively. ![]() and
and ![]() are the slowness vectors at the source and receiver points respectively.
are the slowness vectors at the source and receiver points respectively.
This inversion formula is only valid in the high-frequency limit. Under such
circumstances, it is better to process data for the upward normal derivative
![]() at each discontinuity surface of
at each discontinuity surface of
![]() .
. ![]() is a sum of
weighted singular functions with peaks on the reflectors. Therefore,
is a sum of
weighted singular functions with peaks on the reflectors. Therefore,
![]() actually provides an image of the
subsurface. Using the Fourier transform, we can obtain the following 2.5-D
formula for
actually provides an image of the
subsurface. Using the Fourier transform, we can obtain the following 2.5-D
formula for ![]() .
.
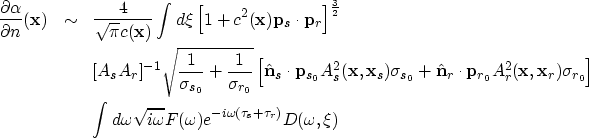 |
||
| (7) |
Bleistein et al.1987 also shows that
![]() can be
related to the reflection coefficient on the interface by
can be
related to the reflection coefficient on the interface by
| (8) |
![]() in the singular function of the model space.
in the singular function of the model space.
![]() is determined by the changes of velocity and
density above and below the interface and the incident angle on the
interface
is determined by the changes of velocity and
density above and below the interface and the incident angle on the
interface
 |
(9) |
In order to determine ![]() from
from
![]() , we have to determine
, we have to determine ![]() .
In their paper, Bleistein et al.1987 proposed
another inversion operator
.
In their paper, Bleistein et al.1987 proposed
another inversion operator
![]() with a kernel slightly modified from that in
with a kernel slightly modified from that in
![]() .
.
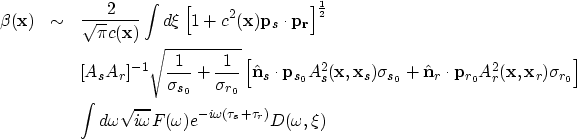 |
||
| (10) |
There is a simple relation between ![]() ,
,
![]() , and
, and ![]() , that is
, that is
| (11) |
With ![]() known, we can use
known, we can use ![]() and
and ![]() to calculate the reflection coefficient
to calculate the reflection coefficient ![]() .
From
.
From ![]() and
and ![]() , we can further estimate
the AVO coefficients: intercept and slope.
, we can further estimate
the AVO coefficients: intercept and slope.
Instead of using ![]() and
and ![]() ,
we propose another pair of inversion operators that can determine
,
we propose another pair of inversion operators that can determine
![]() in a similar, but more straightforward and physically
meaningful manner.
The first operator gives the reflection coefficient at
the specular incident angle
in a similar, but more straightforward and physically
meaningful manner.
The first operator gives the reflection coefficient at
the specular incident angle
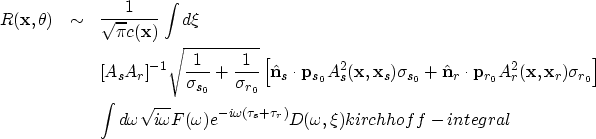 |
||
| (12) |
The second gives the reflection coefficient multiplied by ![]()
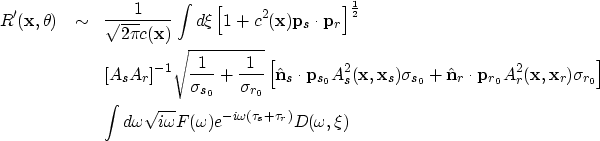 |
||
| (13) |
From ![]() and
and ![]() , we can
easily calculate
, we can
easily calculate ![]()
| (14) |
In order to reduce the sensitivity of ![]() to noise in the data,
we use a least-squares procedures to estimate
to noise in the data,
we use a least-squares procedures to estimate ![]() . First, we define
a small window (nx
. First, we define
a small window (nx ![]() nz). Within the window, we can get a series
of equations
nz). Within the window, we can get a series
of equations
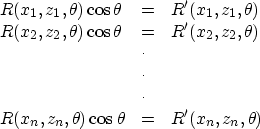 |
(15) |
the least-squares sense estimate of ![]() is then
is then
| (16) |