![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)




Next: MORE EQUATIONS THAN UNKNOWNS
Up: Table of Contents
Data modeling by least squares
The reconciliation of theory
and data is the essence of science.
An ubiquitous tool in this task
is the method of least-squares fitting.
Elementary calculus books generally consider
the fitting of a straight line to scattered
data points.
Such an elementary application
gives scant hint of the variety of
practical problems which can be solved
by the method of least squares.
Some geophysical examples which we will consider
include locating earthquakes,
analyzing tides,
expanding the earth's gravity and magnetic fields in spherical
harmonics, and doing interesting things with time series.
When the past of a time series is available,
one may find that least squares can be used to
determine a filter which predicts
some future values of the time series.
When a time series which has been
highly predictable for a long stretch of time
suddenly becomes much less predictable an
``event'' is said to have occurred.
A filter which emphasizes such events is called
a prediction-error filter.
If one is searching for a particular dispersed wavelet
in a time series, it may help to design a filter
which compresses the wavelet into some more recognizable
shape, an impulse for example.
Such a wave-shaping filter may
be designed by least squares.
With multiple time series which arise from
several sensors detecting waves in space,
least squares may be used to find filters
which respond only to certain directions and wave speeds.
Before we begin with the general theory,
let us take up a simple example in
the subject of time series analysis.
Given the input, say 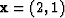 to some filter,
say
to some filter,
say 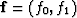 then the output is necessarily
then the output is necessarily
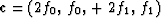 .
To design an inverse filter
we would wish to have c
come out as close as possible to
.
To design an inverse filter
we would wish to have c
come out as close as possible to 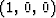 .
In order to minimize the difference between the actual and
the desired outputs we minimize
.
In order to minimize the difference between the actual and
the desired outputs we minimize
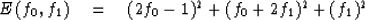
The sum E of the squared errors
will attain a minimum if f0 and f1
are chosen so that
Canceling a 2 and arranging this into
the standard form for simultaneous equations, we get
![\begin{displaymath}
\left[
\begin{array}
{cc}
5 & 2 \\ 2 & 5 \end{array} \rig...
...t]
\eq \left[
\begin{array}
{c}
2 \\ 0 \end{array} \right] \end{displaymath}](img7.gif)
and the solution is
![\begin{displaymath}
\left[
\begin{array}
{c}
f_0 \\ f_1 \end{array} \right]
...
...rray}
{r}
{10 \over 21} \\ -{4 \over 21} \end{array} \right] \end{displaymath}](img8.gif)
The actual  which comes out of this filter
is
which comes out of this filter
is 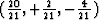 which is not a bad approximation to (1, 0, 0).
which is not a bad approximation to (1, 0, 0).
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)




Next: MORE EQUATIONS THAN UNKNOWNS
Up: Table of Contents
Stanford Exploration Project
10/30/1997
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![]() to some filter,
say
to some filter,
say ![]() then the output is necessarily
then the output is necessarily
![]() .
To design an inverse filter
we would wish to have c
come out as close as possible to
.
To design an inverse filter
we would wish to have c
come out as close as possible to ![]() .
In order to minimize the difference between the actual and
the desired outputs we minimize
.
In order to minimize the difference between the actual and
the desired outputs we minimize
![]()
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)