




Next: About this document ...
Up: Mathematical physics in stratified
Previous: CONSERVATION PRINCIPLES AND MODE
It is now presumed that the reader has a general knowledge
of classical elasticity theory.
Few textbooks, if any, develop the special subject of stratified media
which is so important in seismology.
Many papers on that subject may be found in the
Bulletin of the Seismological Society of America (BSSA).
For those readers unfamiliar with the BSSA,
we now present the results of applying the general methods of this chapter
to the equations of isotropic elasticity.
The conventions in elasticity are (u, w) displacements
in x and z directions,
 is the stress matrix,
is the stress matrix,
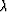 and
and 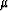 are Lame's constants and
are Lame's constants and 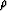 is density.
Hooke's law and Newton's law with
is density.
Hooke's law and Newton's law with 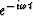 time dependence leads to
time dependence leads to
| ![\begin{displaymath}
\frac{\partial}{\partial z}\, \left[ \begin{array}
{l} U \\ ...
...array}
{l} U\\ \tau_{zz} \\ W \\ \tau_{zx}\end{array}\right]\end{displaymath}](img183.gif) |
(1) |
where
| 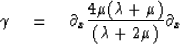 |
(2) |
Define also
| 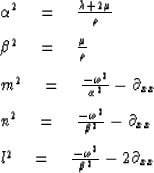 |
(3) |
If material properties do not vary in the x direction,
we have the row eigenvector transformation
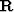 to up- and downgoing wave variables.
to up- and downgoing wave variables.
| ![\begin{displaymath}
\left[ \begin{array}
{l} p^{+} \\ s^{+} \\ p^{-} \\ s^{-}...
...ray}
{l} u \\ \tau_{zz} \\ w \\ \tau_{zx} \end{array}\right]\end{displaymath}](img186.gif) |
(4) |
and the column eigenvector inverse transform 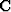
| ![\begin{displaymath}
\left[ \begin{array}
{l} u \\ \tau_{zz} \\ w \\ \tau_{zx}...
...ray}
{l} p^{+} \\ s^{+} \\ p^{-} \\ s^{-} \end{array}\right]\end{displaymath}](img187.gif) |
(5) |
where
![\begin{displaymath}
\Lambda = \left[ \begin{array}
{llll} m & & & \\ & n & & \\ & & -m & \\ & & & -n \end{array} \right] \end{displaymath}](img188.gif)
The matrices partition nicely into 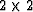 blocks.
The reader may verify
that
blocks.
The reader may verify
that 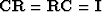 and
and 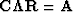 .
.





Next: About this document ...
Up: Mathematical physics in stratified
Previous: CONSERVATION PRINCIPLES AND MODE
Stanford Exploration Project
10/30/1997
![]() is the stress matrix,
is the stress matrix,
![]() and
and ![]() are Lame's constants and
are Lame's constants and ![]() is density.
Hooke's law and Newton's law with
is density.
Hooke's law and Newton's law with ![]() time dependence leads to
time dependence leads to
![\begin{displaymath}
\frac{\partial}{\partial z}\, \left[ \begin{array}
{l} U \\ ...
...array}
{l} U\\ \tau_{zz} \\ W \\ \tau_{zx}\end{array}\right]\end{displaymath}](img183.gif)
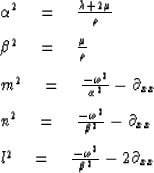
![\begin{displaymath}
\left[ \begin{array}
{l} p^{+} \\ s^{+} \\ p^{-} \\ s^{-}...
...ray}
{l} u \\ \tau_{zz} \\ w \\ \tau_{zx} \end{array}\right]\end{displaymath}](img186.gif)
![\begin{displaymath}
\left[ \begin{array}
{l} u \\ \tau_{zz} \\ w \\ \tau_{zx}...
...ray}
{l} p^{+} \\ s^{+} \\ p^{-} \\ s^{-} \end{array}\right]\end{displaymath}](img187.gif)
![\begin{displaymath}
\Lambda = \left[ \begin{array}
{llll} m & & & \\ & n & & \\ & & -m & \\ & & & -n \end{array} \right] \end{displaymath}](img188.gif)