




Next: Sign convention
Up: Model fitting by least
Previous: Unknown input: deconvolution with
The solution time for simultaneous linear equations
grows cubically with the number of unknowns.
There are three regimes for solution;
which one is applicable
depends on the number of unknowns m.
For m three or less, we use analytical methods.
We also sometimes use analytical methods on matrices of size 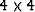 when the matrix contains enough zeros.
Today in year 2001,
a deskside workstation, working an hour solves about a
when the matrix contains enough zeros.
Today in year 2001,
a deskside workstation, working an hour solves about a
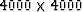 set of simultaneous equations.
A square image packed into a 4096 point vector is a
set of simultaneous equations.
A square image packed into a 4096 point vector is a 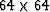 array.
The computer power for linear algebra to give us solutions that
fit in a
array.
The computer power for linear algebra to give us solutions that
fit in a 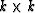 image is thus proportional
to k6, which means that even though computer power grows rapidly,
imaging resolution using ``exact numerical methods'' hardly
grows at all from our
image is thus proportional
to k6, which means that even though computer power grows rapidly,
imaging resolution using ``exact numerical methods'' hardly
grows at all from our 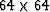 current practical limit.
current practical limit.
The retina in our eyes captures an image of size about 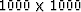 which is a lot bigger than
which is a lot bigger than 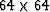 .Life offers us many occasions where final images exceed the 4000
points of a
.Life offers us many occasions where final images exceed the 4000
points of a 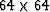 array.
To make linear algebra (and inverse theory) relevant to such problems,
we investigate special techniques.
A numerical technique known as the
``conjugate-direction method''
works well for all values of m and is our subject here.
As with most simultaneous equation solvers,
an exact answer (assuming exact arithmetic)
is attained in a finite number of steps.
And if n and m are too large to allow enough iterations,
the iterative methods can be interrupted at any stage,
the partial result often proving useful.
Whether or not a partial result actually is useful
is the subject of much research;
naturally, the results vary from one application to the next.
array.
To make linear algebra (and inverse theory) relevant to such problems,
we investigate special techniques.
A numerical technique known as the
``conjugate-direction method''
works well for all values of m and is our subject here.
As with most simultaneous equation solvers,
an exact answer (assuming exact arithmetic)
is attained in a finite number of steps.
And if n and m are too large to allow enough iterations,
the iterative methods can be interrupted at any stage,
the partial result often proving useful.
Whether or not a partial result actually is useful
is the subject of much research;
naturally, the results vary from one application to the next.
![]() which is a lot bigger than
which is a lot bigger than ![]() .Life offers us many occasions where final images exceed the 4000
points of a
.Life offers us many occasions where final images exceed the 4000
points of a ![]() array.
To make linear algebra (and inverse theory) relevant to such problems,
we investigate special techniques.
A numerical technique known as the
``conjugate-direction method''
works well for all values of m and is our subject here.
As with most simultaneous equation solvers,
an exact answer (assuming exact arithmetic)
is attained in a finite number of steps.
And if n and m are too large to allow enough iterations,
the iterative methods can be interrupted at any stage,
the partial result often proving useful.
Whether or not a partial result actually is useful
is the subject of much research;
naturally, the results vary from one application to the next.
array.
To make linear algebra (and inverse theory) relevant to such problems,
we investigate special techniques.
A numerical technique known as the
``conjugate-direction method''
works well for all values of m and is our subject here.
As with most simultaneous equation solvers,
an exact answer (assuming exact arithmetic)
is attained in a finite number of steps.
And if n and m are too large to allow enough iterations,
the iterative methods can be interrupted at any stage,
the partial result often proving useful.
Whether or not a partial result actually is useful
is the subject of much research;
naturally, the results vary from one application to the next.