




Next: NOISE BURSTS
Up: MEANS, MEDIANS, PERCENTILES AND
Previous: Nonlinear L.S. conjugate-direction template
Cauchy function
A good trick
(I discovered accidentally) is to use the weight
|  |
(16) |
Sergey Fomel points out that this weight arises from
minimizing the Cauchy function:
|  |
(17) |
A plot of this function is found in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
cauchy
.
cauchy
Figure 2
The coordinate is m.
Top is Cauchy measures of m-1.
Bottom is the same measures of the data set (1,1,2,3,5).
Left, center, and right are for
 .
.





Because the second derivative is not positive everywhere,
the Cauchy function introduces the possibility of multiple solutions,
but because of the good results we see in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
you might like to try it anyway.
Perhaps the reason it seems to work so well is that
it uses mostly residuals of ``average size,''
not the big ones or the small ones.
This happens because
,
you might like to try it anyway.
Perhaps the reason it seems to work so well is that
it uses mostly residuals of ``average size,''
not the big ones or the small ones.
This happens because  is made from
is made from  and
the components of
and
the components of  which are a function
which are a function
 that is maximum for those residuals near
that is maximum for those residuals near
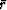 .
.
Module irls ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) supplies two useful
weighting functions that can be interchanged as arguments to the
reweighted scheme
supplies two useful
weighting functions that can be interchanged as arguments to the
reweighted scheme ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
irlsweighting functions for iterative reweighting
.
irlsweighting functions for iterative reweighting





Next: NOISE BURSTS
Up: MEANS, MEDIANS, PERCENTILES AND
Previous: Nonlinear L.S. conjugate-direction template
Stanford Exploration Project
4/27/2004


![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
you might like to try it anyway.
Perhaps the reason it seems to work so well is that
it uses mostly residuals of ``average size,''
not the big ones or the small ones.
This happens because
,
you might like to try it anyway.
Perhaps the reason it seems to work so well is that
it uses mostly residuals of ``average size,''
not the big ones or the small ones.
This happens because ![]() is made from
is made from ![]() and
the components of
and
the components of ![]() which are a function
which are a function
![]() that is maximum for those residuals near
that is maximum for those residuals near
![]() .
.![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) supplies two useful
weighting functions that can be interchanged as arguments to the
reweighted scheme
supplies two useful
weighting functions that can be interchanged as arguments to the
reweighted scheme ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
irlsweighting functions for iterative reweighting
.
irlsweighting functions for iterative reweighting