Preconditioner with a starting guess

In many applications, for many reasons, we have a starting guess $\bold m_0$ of the solution. You might worry that you could not find the starting preconditioned variable $\bold p_0= \bold S^{-1}\bold m_0$because you did not know the inverse of 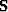$\bold S$.The way to avoid this problem is to reformulate the problem in terms of a new variable $\tilde {\bold m}$where $\bold m = \tilde {\bold m} + \bold m_0$.Then $\bold 0\approx \bold F \bold m - \bold d$becomes $\bold 0\approx \bold F \tilde {\bold m} - (\bold d - \bold F \bold m_0)$or $\bold 0\approx \bold F \tilde {\bold m} - \tilde {\bold d}.$Thus we have accomplished the goal of taking a problem with a nonzero starting model and converting it a problem of the same type with a zero starting model. 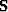Thus we do not need the inverse of $\bold S$because the iteration starts from $\tilde {\bold m}=\bold 0$so $\bold p_0 = \bold 0$.