




Next: OPPORTUNITIES FOR SMART DIRECTIONS
Up: PRECONDITIONING THE REGULARIZATION
Previous: Statistical interpretation
Summing up the ideas above,
we start from fitting goals
|  |
(8) |
and we change variables from
 to
to 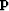 using
using

|  |
(9) |
Preconditioning means iteratively fitting
by adjusting the 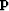 variables
and then finding the model by using
variables
and then finding the model by using
 .A new reusable
preconditioned solver is
the module solver_prc
.A new reusable
preconditioned solver is
the module solver_prc ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Likewise the modeling operator
.
Likewise the modeling operator  is called Fop
and the smoothing operator
is called Fop
and the smoothing operator  is called Sop.
Details of the code are only slightly different from
the regularized solver
solver_reg
is called Sop.
Details of the code are only slightly different from
the regularized solver
solver_reg ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
solver_prcPreconditioned solver
.
solver_prcPreconditioned solver





Next: OPPORTUNITIES FOR SMART DIRECTIONS
Up: PRECONDITIONING THE REGULARIZATION
Previous: Statistical interpretation
Stanford Exploration Project
4/27/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Likewise the modeling operator
.
Likewise the modeling operator ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
solver_prcPreconditioned solver
.
solver_prcPreconditioned solver