 |
(8) |
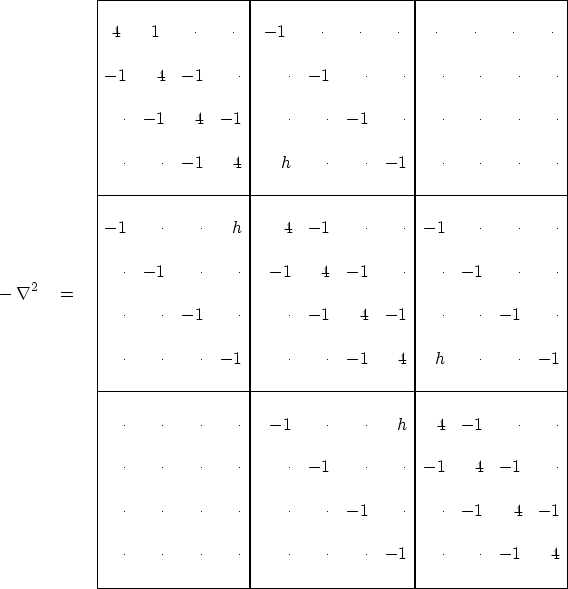
The two-dimensional matrix of coefficients for the Laplacian operator
is shown in (8),
where,
on a Cartesian space, h=0,
and in the helix geometry, h=-1.
(A similar partitioned matrix arises from packing
a cylindrical surface into a ![]() array.)
Notice that the partitioning becomes transparent for the helix, h=-1.
With the partitioning thus invisible, the matrix
simply represents one-dimensional convolution
and we have an alternative analytical approach,
one-dimensional Fourier Transform.
We often need to solve sets of simultaneous equations
with a matrix similar to (8).
The method we use is triangular factorization.
array.)
Notice that the partitioning becomes transparent for the helix, h=-1.
With the partitioning thus invisible, the matrix
simply represents one-dimensional convolution
and we have an alternative analytical approach,
one-dimensional Fourier Transform.
We often need to solve sets of simultaneous equations
with a matrix similar to (8).
The method we use is triangular factorization.
Although the autocorrelation ![]() has mostly zero values,
the factored autocorrelation
has mostly zero values,
the factored autocorrelation ![]() from (5)
has a great number of nonzero terms,
but fortunately they seem to be converging rapidly (in the middle)
so truncation (of the middle coefficients) seems reasonable.
I wish I could show you a larger matrix, but all I can do is to pack
the signal
from (5)
has a great number of nonzero terms,
but fortunately they seem to be converging rapidly (in the middle)
so truncation (of the middle coefficients) seems reasonable.
I wish I could show you a larger matrix, but all I can do is to pack
the signal ![]() into shifted columns of
a lower triangular matrix
into shifted columns of
a lower triangular matrix ![]() like this:
like this:
![\begin{displaymath}
\bold H \ = \ \
\left[
\begin{array}
{rrrrrrrrrrrr}
1.8&\cd...
...ot&\cdot&\cdot&\cdot& -.6& -.2& 0.0& -.6& 1.8\end{array}\right]\end{displaymath}](img46.gif) |
(9) |