# convolution: Y(Z) = X(Z) * B(Z)
#
subroutine convolve( nb, bb, nx, xx, yy )
integer nb # number of coefficients in filter
integer nx # number of coefficients in input
# number of coefficients in output will be nx+nb-1
real bb(nb) # filter coefficients
real xx(nx) # input trace
real yy(1) # output trace
integer ib, ix, iy, ny
ny = nx + nb -1
call null( yy, ny)
do ib= 1, nb
do ix= 1, nx
yy( ix+ib-1) = yy( ix+ib-1) + xx(ix) * bb(ib)
return; end
This program is written in a language called Ratfor,
a ``rational'' dialect of Fortran.
It is similar to the Matlab language.
You are not responsible for anything in this program,
but, if you are interested,
more details in the last chapter of PVI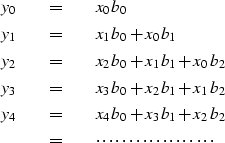
![\begin{displaymath}
\left[
\begin{array}
{c}
y_0 \\
y_1 \\
y_2 \\
y_3...
...
\begin{array}
{c}
b_0 \\
b_1 \\
b_2 \end{array} \right]\end{displaymath}](img18.gif)
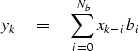
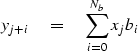
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) ,
the book that I condensed this from.
,
the book that I condensed this from.