 |
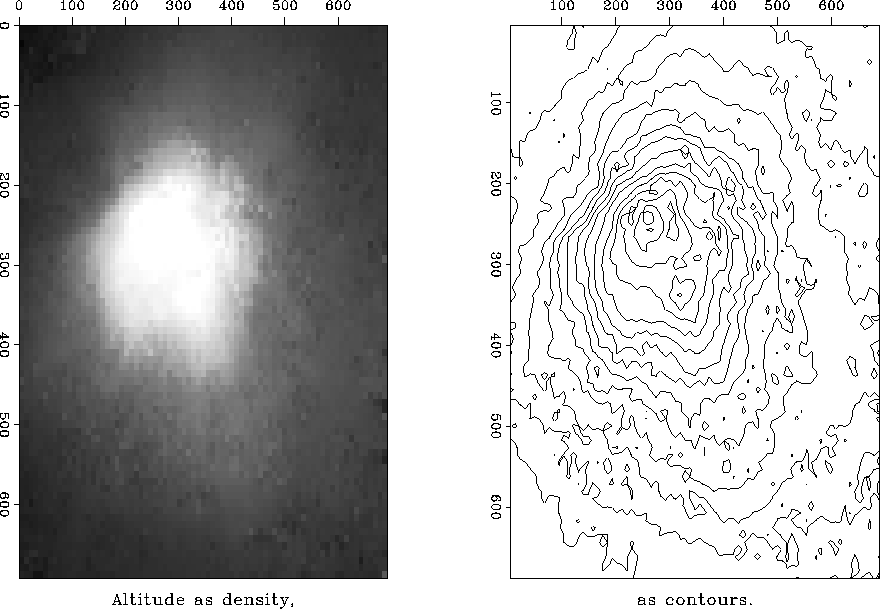
Figure 5 Estimated altitude.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
invstack()
and
invstack() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
module unwrap {
use cgstep_mod
use igrad2
use simple_solver
contains
subroutine grad2init( z,n1,n2, rt ) {
integer i, j, n1,n2
real rt( n1,n2,2)
complex z(n1,n2), a,b,c
rt = 0.
do i= 1, n1-1 {
do j= 1, n2-1 {
a = z(i ,j )
c = z(i+1,j ); rt(i,j,1) = aimag( clog( c * conjg( a) ) )
b = z(i, j+1); rt(i,j,2) = aimag( clog( b * conjg( a) ) )
}}
}
# Phase unwraper. Starting from phase h, improve it.
subroutine unwraper( zz, hh, niter) {
integer n1,n2, niter
complex zz(:,:)
real hh(:)
real, allocatable :: rt(:)
n1 = size (zz, 1)
n2 = size (zz, 2)
allocate( rt (n1*n2*2))
call grad2init( zz,n1,n2,rt)
call igrad2_init( n1,n2)
call solver( igrad2_lop, cgstep, hh, rt, niter, x0 = hh)
call cgstep_close ()
deallocate( rt)
}
}
An open question is whether the required number of iterations is reasonable or whether we would need to uncover a preconditioner or more rapid solution method. I adjusted the frame size (by the amount of smoothing in Figure 3) so that I would get the solution in about ten seconds with 400 iterations. Results are shown in Figure 5.
 |