Noise Free Data

Assume that the data S are model-consistent, that is

$$S(t,x)=r^*(T_0^*(t,x)) + O(\lambda)$$

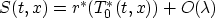
for target offset independent reflectivity r^*(t₀) and velocity v^*(t₀). [Since differential semblance does not depend to leading order on the amplitude, as noted above, I set the amplitude to 1 in the following, for simplicity - it can be reintroduced with almost no change in the results to follow.]

Note that

$$0=\frac{\partial}{\partial x}T(T_0(t,x),x)= \frac{\partial ... ..._0}{\partial x}(t,x) +\frac{\partial T}{\partial x}(T_0(t,x),x)$$

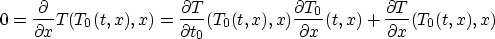
so

$$\frac{\partial T_0}{\partial x}(t,x)=-s(t,x)p(t,x)$$

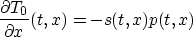
(s being the stretch factor, defined above). Thus

$$\frac{\partial}{\partial x}r^*(T_0^*(t,x)) = -s^*(t,x)p^*(t,x) (\frac{\partial r^*}{\partial t_0})(T_0^*(t,x))$$

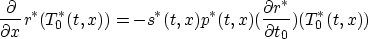
(s^* is the stretch factor belonging to v^*) whence

$$F[v]WG[v]S(t,x)=\left(\frac{\partial}{\partial x}+p(t,x) \frac{\partial}{\partial t}\right)r^*(T_0^*(t,x))$$

$$=s^*(t,x) (p(t,x)-p^*(t,x))\frac{\partial r^*}{\partial t_0}(T_0^*(t,x))$$

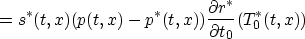
According to the calculus of pseudodifferential operators,

$$H \phi F[v]WG[v]S =$$

$$(I-\nabla^2)^{-\frac{1}{2}}\phi \left(s^*(p-p^*)\frac{\partial r^*}{\partial t_0}(T_0^*)\right)$$

$$=(I-\nabla^2)^{-\frac{1}{2}}\phi \left(s^*(p-p^*)\frac{\nabl... ...cdot \nabla}{\nabla T_0^* \cdot \nabla T_0^*}r^*(T_0^*)\right)$$

$$=\phi \frac{s^*(p-p^*)}{\sqrt{1+s^{*,2}(1+p^{*,2})}}r^*(T_0^*)+O(\lambda)$$

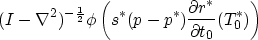
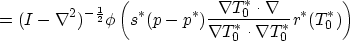
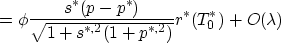
where you get from the next to the last line to the last by substituting 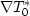$\nabla T_0^*$ for $\nabla$, and using previously derived formulas for the partial derivatives of T₀.

Thus

$$J_0[v]=\int\int \,dt\,dx\, B^*(t,x)(p(t,x)-p^*(t,x))^2 [r^*(T_0^*(t,x))]^2 +O(\lambda)$$

where

$$B^*(t,x)=\phi^2 \frac{s^{*,2}}{1+s^{*,2}(1+p^{*,2})}$$

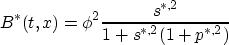
is independent of v, i.e. depending only on v^* and $\cal{A}$.

In the next section I introduce the so called hyperbolic moveout approximation to traveltime. Note that up to this point the development is entirely independent of this approximation. In particular the formulas worked out in this section have precise analogues for versions of differential semblance based on multidimensional seismic models.