Next: An example of inversion
Up: Biondi & Sava: Wave-equation
Previous: Perturbation field: Adjoint operator
This section offers a pictorial description of the
theory presented in the preceding section. We use two simple
examples to highlight the main features of the method. In both cases,
the reflectivity model consists of two flat interfaces, one shallow
and one deep. The velocity models are different as follows:
-
In the first model, we started with a constant velocity background of
2 km/s, on which we superimposed a positive Gaussian perturbation with
a magnitude of 0.25 km/s, as shown in the right panel of
Figure 2.
-
In the second model, we superimposed a negative Gaussian anomaly with
the magnitude of 0.5 km/s on the background velocity
(Figure 2), while the perturbation remained the same as in
the first model (the right panel of Figure 2). The main
purpose of selecting this second velocity model was to demonstrate the
robustness of the forward and adjoint operators to triplications in
the wavefield.
slow
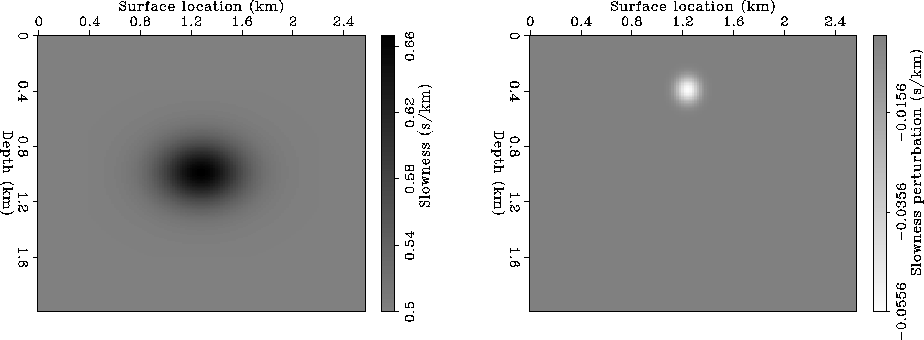
Figure 2
Background slowness (labeled S in
Figure 1) - left;
Perturbation in slowness (labeled 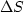 in
Figure 1) - right.
in
Figure 1) - right.
 data
data
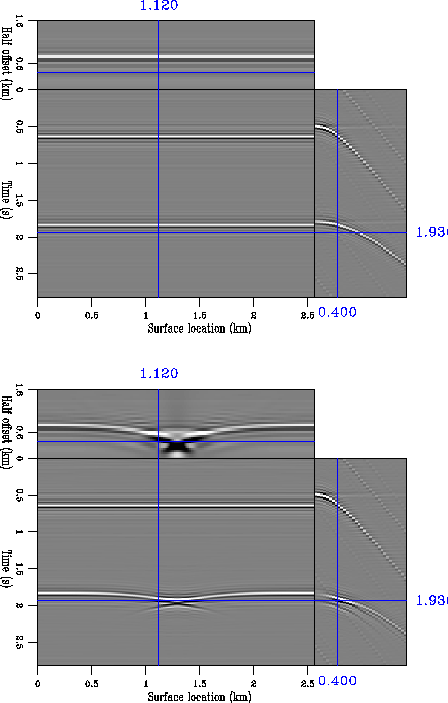
Figure 3
The data (labeled D in Figure 1) measured at the
surface for each of the background velocity models.
The top panel corresponds to the case of the constant background
velocity, while the bottom panel corresponds to the case of the
Gaussian anomaly in the background velocity.





image
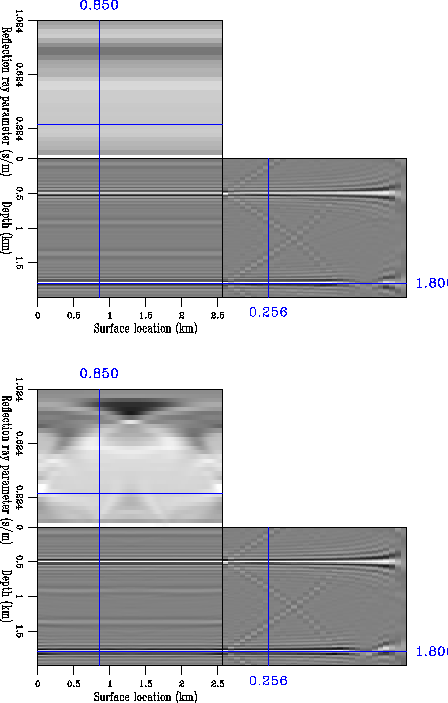
Figure 4
The image (labeled R in Figure 1) obtained after
migrating by downward continuation the data in Figure 3.
The top panel corresponds to the case of the constant background
velocity, while the bottom panel corresponds to the case of the
Gaussian anomaly in the background velocity.





dimage
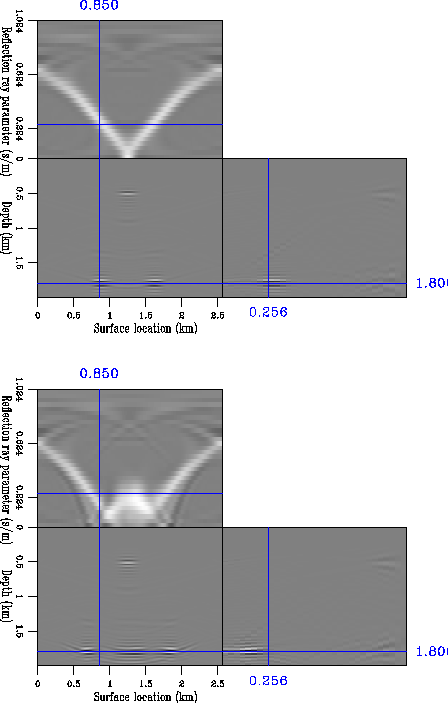
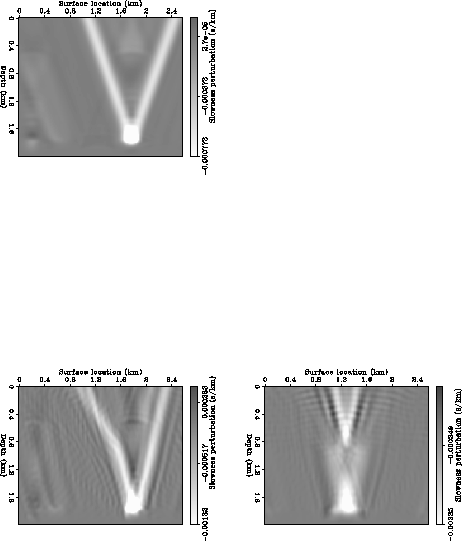
Figure 5
The perturbation in image (labeled 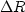 in
Figure 1), that is, the data migrated with the
perturbation in slowness.
The top panel corresponds to the case of the constant background
velocity (Kjartansson's V), while the bottom panel corresponds to the
case of the Gaussian anomaly in the background velocity.
in
Figure 1), that is, the data migrated with the
perturbation in slowness.
The top panel corresponds to the case of the constant background
velocity (Kjartansson's V), while the bottom panel corresponds to the
case of the Gaussian anomaly in the background velocity.





rays
Figure 6
The perturbation in slowness (labeled 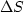 in
Figure 1) corresponding to part of the perturbation in
image (Figure 5). The ``fat rays'' are the result of the
back-projection of the perturbation in slowness.
The top panel corresponds to the case of the constant background
velocity, while the bottom panel corresponds to the case of the
Gaussian anomaly in the background velocity.
in
Figure 1) corresponding to part of the perturbation in
image (Figure 5). The ``fat rays'' are the result of the
back-projection of the perturbation in slowness.
The top panel corresponds to the case of the constant background
velocity, while the bottom panel corresponds to the case of the
Gaussian anomaly in the background velocity.





We started by creating the synthetic data (D) that correspond to each
of the individual models (Figure 3). In the
second case, the reflection from the deeper interface creates a
triplication caused by the Gaussian anomaly in the background
velocity.
Then, we migrated the synthetic data using the correct velocity models
in each case, and obtained the background images (R)
shown in Figure 4.
We then repeated the same succession of operations, considering the
background velocity models on which we superimposed the perturbation
anomaly. We then created the data and migrated it with the
perturbation in slowness. What we obtained is the perturbation in
image depicted in Figure 5.
The shape of the image at a given depth is known in the literature as
Kjartansson's V Kjartansson (1979).
In the case of the nonconstant
background, the triplications of the wavefield created a more complex
perturbation in the image, which is especially visible at the level of
the deeper reflector. For this case, Kjartansson's V becomes a W
(Figure 5).
Finally, we back-projected into the velocity model the
perturbations we obtained in the images (Figure 6).
To clarify how the back-projection operator works, we have isolated
in each panel a single event of the perturbation in image, for a fixed
reflection ray parameter.
As expected, we have obtained ``fat rays'' showing which regions of
the velocity model are influenced by the perturbation in image. The
top panel of Figure 6 displays the straight fat rays
corresponding to the constant velocity background. The bottom
left panel, shows the rays for a similar perturbation in the image as
in the first case, while the bottom right panel displays the rays for
the perturbation in image in a region where the wavefield has
triplicated when propagating through the anomaly in the background.





Next: An example of inversion
Up: Biondi & Sava: Wave-equation
Previous: Perturbation field: Adjoint operator
Stanford Exploration Project
6/1/1999