The amplitude satisfies the zeroth order transport equation Cervený et al. (1977):
| |
(3) |
If the traveltime field has been found by solving the eikonal equation, then equation (3) is a first order advection equation. However, we see that the Laplacian of traveltime field is involved in the transport equation, which implies that we need a third order accurate traveltime field to get a first order accurate amplitude field El-Mageed et al. (1997); El-Mageed (1996); Symes (1995). To avoid this complexity, we use another approach to compute the amplitude.
In 2D isotropic media, the amplitude satisfies Cervený et al. (1977); Friedlander (1958)
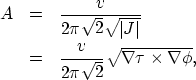 |
||
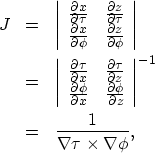 |
||
Since the take-off angle ![]() is constant along any ray,
is constant along any ray,
| (4) |
However, the gradient of the take-off angle depends on the second order derivative of traveltime, so that we need third order accurate traveltimes to get a first order accurate gradient of take-off angle. Zhang 1993 used this equation in polar coordinates to compute the geometrical spreading factor, but his computation of the take-off angle was based on the first order traveltime field. Consequently, the gradient of take-off angle computed by his scheme was inaccurate. Vidale 1990 encountered a similar difficulty.