WENO for advection equations

Recall the advection equation for the take-off angle,

$$\begin{eqnarray} \frac{\partial \tau}{\partial x}\frac{\partial \phi}{\partial x... ...\tau}{\partial z}\frac{\partial \phi}{\partial z} &=& 0. \nonumber\end{eqnarray}$$

To match with the evolutionary form of the eikonal equation in depth, we formulate the advection equation as an evolution equation in depth as well, i.e.,

$$\begin{eqnarray} \frac{\partial \phi}{\partial z}&=&-(\frac{\partial \tau}{\part... ...}\frac{\partial \tau}{\partial x}\frac{\partial \phi}{\partial x}.\end{eqnarray}$$ (8)

To take advantage of the accuracy of traveltime provided by an ENO (or WENO) Runge-Kutta third order scheme for eikonal equation, we embed the third order scheme for equation (8) into the third order scheme for the eikonal equation.

To be more precise, we introduce the approximations for x-derivative and z-derivative of $\tau$ in the above advection equation:

$$\begin{eqnarray} \frac{\partial \tau}{\partial x}\approx \widehat{D}_{x}^{5}\tau... ...ax}(\max (D_{x}^{-,5}\tau,0),\min (D_{x}^{+,5}\tau,0)), \nonumber \end{eqnarray}$$

$$\begin{eqnarray} \frac{\partial \tau}{\partial z}&\approx&H(\widehat{D}_{x}^{5}\tau).\nonumber \end{eqnarray}$$

However, we must be careful in defining the upwind ENO difference approximation for $\frac{\partial \phi}{\partial x}$ because the ENO choice of stencil is too sensitive to the zeros of solution Jiang and Shu (1996); Liu et al. (1994). Instead, we will use a weighted ENO (WENO) scheme to approximate the derivative. Because the coefficient of the discretized advection equation has only second order accuracy, which is computed from the eikonal equation by the third order scheme, we use a third order WENO scheme to approximate the derivative $\frac{\partial \phi}{\partial x}$. The third order WENO scheme is based on the second order ENO stencils, so it does not give rise to any new complexities in the coding.

The third order upwind WENO approximations to $\frac{\partial \phi}{\partial x}$ Jiang and Peng (1997) are

$$\begin{eqnarray} \left(\frac{\partial \phi}{\partial x}\right)_{i}^{k} \approx (... ...1}^{k}-2 D_{x}^{+}\phi_{i}^{k}+D_{x}^{+}\phi_{i-1}^{k}), \nonumber\end{eqnarray}$$

where

$$\begin{eqnarray} w_{-} &=& \frac{1}{1+2r_{-}^{2}}, r_{-} = \frac{\delta+(D^{-}D^... ...\phi_{i}^{k})^{2}}{\delta+(D^{-}D^{+}\phi_{i}^{k})^{2}}, \nonumber\end{eqnarray}$$

and $\delta$ is a small positive constant to prevent the denominators from becoming zero.

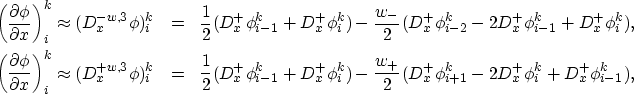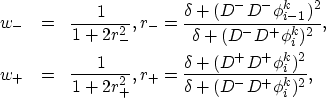Now we define the upwind WENO difference for $\frac{\partial \phi}{\partial x}$, which corresponds to the upwind direction of $\frac{\partial \tau}{\partial x}$ as follows:

$$\begin{eqnarray} D_{x}^{up}\phi_{i}^{k}&=&\left\{ \begin{array} {lll} D_{x}^{-w... ...}^{+w,3}\phi_{i}^{k} & \mbox{else}. \end{array} \right. \nonumber\end{eqnarray}$$

Finally, we can formulate the third order WENO Runge-Kutta scheme for the advection equation as

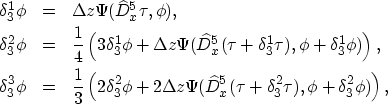$$\begin{eqnarray} \delta_{3}^{1}\phi&=&\Delta{z}\Psi(\widehat{D}_{x}^{5}\tau,\phi... ...{x}^{5}(\tau+\delta_{3}^{2}\tau),\phi+\delta_{3}^{2}\phi)\right), \end{eqnarray}$$ (9)

where

$$\begin{eqnarray} \Psi (\tau,\phi)&=& -\frac{\widehat{D}_{x}^{5}\tau D_{x}^{up}\phi}{H(\widehat{D}_{x}^{5}\tau)}. \nonumber\end{eqnarray}$$

The 3rd order scheme for $\phi$ is then

$$\begin{eqnarray} \phi^{k+1}&=&\phi^{k}+\delta_{3}^{3}\phi^{k}\end{eqnarray}$$ (10)

for k=0,1,2,....

But this scheme is really a second order scheme because the coefficients have only second order accuracy.