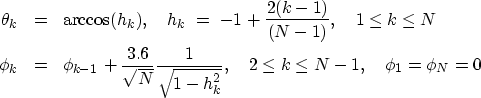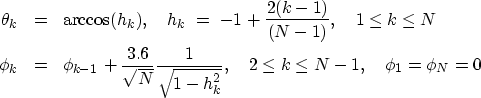Next: Helical coordinate on a
Up: Claerbout: Helical meshes on
Previous: INTRODUCTION
I set out to find the equations describing a rope
that begins from the north pole and spirals its
way around a sphere neatly covering it and ending
at the south pole.
Taking uniform samples along this rope gives
a fairly uniform covering of the sphere.
The surface of a sphere is two dimensional,
but the rope gives a one dimensional covering
that is uniformly sampled in that dimension.
I wondered about the sampling in the other dimension
so I set out to plot it.
I found the ``generalized spiral set''
of Saff and Kuijlaars1997.
In spherical coordinates  , for
, for
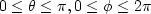 , they set
, they set
| 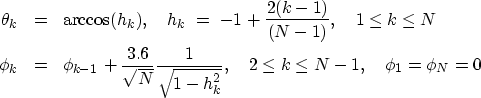 |
(1) |
| (2) |
My plot of these equations is shown in Figure 1.
There is no interesting pattern in the crossline direction.
Although my plot looks reasonable,
Saff and Kuijlaars1997
show a curious pattern in the crossline direction
that my plots do not show.
A few tests with various values of N and various rotations
failed to show any curious pattern.
sphere
Figure 1
Helix on a sphere.
Top shows the embedded helix.
Bottom hides it.
An interesting pattern of points that appears
in the article in the Mathematical Intelligencer
is inexplicably absent here
(even though I tested several rotations and several values of N).










Next: Helical coordinate on a
Up: Claerbout: Helical meshes on
Previous: INTRODUCTION
Stanford Exploration Project
4/20/1999