PEF-Based method

Theoretically, the convolution of data (N_d points) and a PEF (N_a coefficients) estimated from the data is approximately uncorrelated in the limit $N_a \rightarrow N_d \rightarrow \infty$: a spike at zero lag plus Gaussian, independent identically distributed (iid) noise elsewhere. Thus the spectrum of this residual error is approximately white. The frequency response of the ``inverse PEF'', as computed by deconvolution, is an N<sub>a</sub>-point parameterization of the N<sub>d</sub>-point inverse amplitude spectrum, as illustrated in Figure 4. As the size of the filter increases, the parameterization becomes more accurate, as expected from theory Claerbout (1976). The notion of PEF as ``decorrelator'' is quite akin to decomposition by principal components Castleman (1996), where the number of principal components used in computation determines the degree of decorrelation.

 

rand1d-spec Figure 4 Frequency response of ``inverse PEF'' (deconvolution) as a function of filter size. As expected, as the filter length increases, the approximation improves.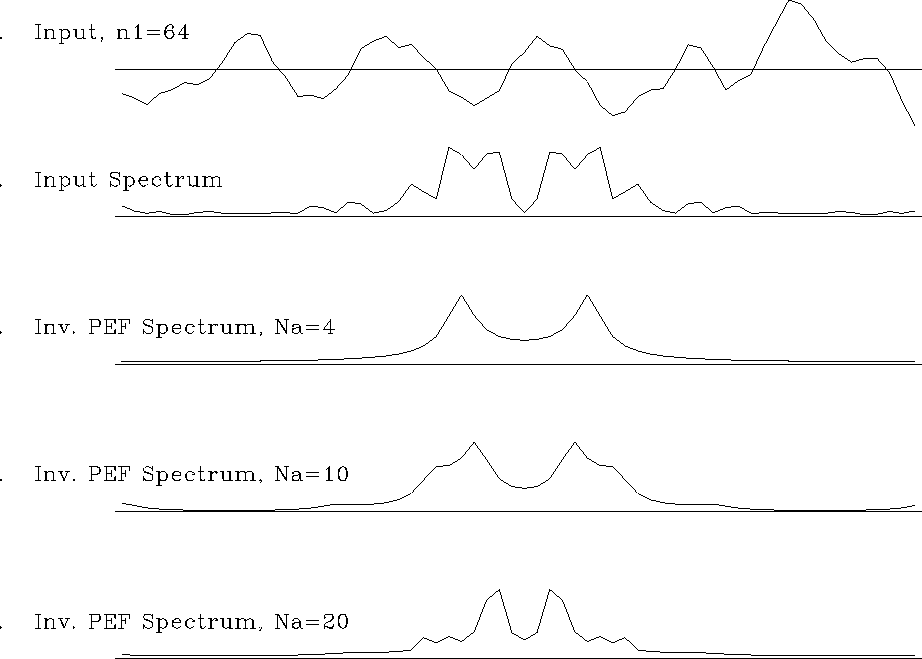

The following is an outline of the PEF-based texture synthesis method.

1.

Given training image t(x,y), estimate unknown PEF a(x,y) via least squares minimization:  

$$\mbox{min} \; \Vert \ t*a \ \Vert^2$$ (3)

2.

The residual r = t*a is approximately uncorrelated, with the same dimension as the TI, since we use an "internal" convolution algorithm Claerbout (1998a). It can be proved that a is a minimum phase filter, Claerbout (1976) so deconvolution (polynomial division) robustly and stably reconstructs t given r.

Generate a random residual r' with the same dimension as r. To create the synthetic texture, simply deconvolve r' by a:  

$$t_{\mbox{\tiny syn}} = r'/a$$ (4)

where the `` / '' refers to polynomial division, our preferred method of deconvolution.

Though the residual is uncorrelated, it does contain ``phase'' information. Deconvolution of a random image blindly spreads scaled copies of the impulse response of the inverse PEF across the output space. If the residual r is not sufficiently whitened, then the replacement of r with r' will lead to an ineffective representation of t by $t_{\mbox{\tiny syn}}$.

Figures 5 through 7 illustrate the PEF-based texture synthesis process. The left-hand panel shows the training image, the center panel shows the residual r = t*a, and the right-hand panel shows the synthesized image, $t_{\mbox{\tiny syn}} = r'/a$. A 10x10 PEF is used in each case. The blank areas in the residual panel correspond to regions where the PEF falls outside the bounds of the known data.

 

rand2d-pefsyn
Figure 5 Smoothed random 2-D image and PEF-based texture synthesis result. The TI is quite simple (stationary, low correlation), so as expected, the synthesized image and the TI are almost indistinguishable. To the naked eye, the residual appears effectively white.

 

ridges-pefsyn
Figure 6 ``Ridges'' image and PEF-based texture synthesis result. Recall that the complicated connected features of this image were not completely synthesized by the Fourier transform method (Figure 3), of which the PEF method is an approximation. This synthesized image bears even less resemblance to the TI, exhibiting only a general southwest-to-northeast trend. The wavy, ridge-like features have many different dips, making them difficult to predict with a PEF, and with two point statistics in general. The same can be said for the ubiquitous hyperbolic features of reflection seismology.

 

wood-pefsyn
Figure 7 ``Wood'' image and PEF-based texture synthesis result. The synthesis result is pleasing. The PEF-based method preserves the general trend and relative scale length of the lineations in the TI. The correlation of the TI is relatively long-range, in that the lineations cross a large portion of the image, but the features are merely straight lines at one dip.