Traveltime considerations

 

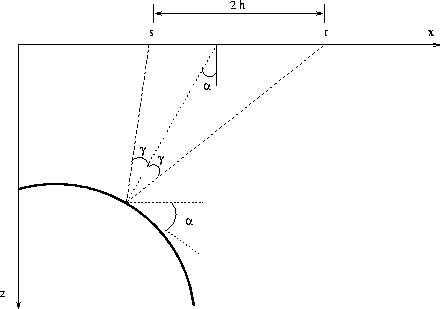rays Figure 1 Reflection rays in a constant-velocity medium: a scheme.

Let us consider a simple reflection experiment in an effectively constant-velocity medium, as depicted in Figure 1. The pair of incident and reflected rays and the line between the source s and the receiver r form a triangle in space. From the trigonometry of that triangle we can derive simple relationships among all the variables of the experiment Fomel (1995, 1996a, 1997).

Introducing the dip angle $\alpha$ and the reflection angle $\gamma$,the total reflection traveltime t can be expressed from the law of sines as  

$$t = \frac{2 h}{v}\, \frac{\cos(\alpha+\gamma) + \cos(\alph... ...\gamma}} = \frac{2 h}{v}\,\frac{\cos{\alpha}}{\sin{\gamma}}\;,$$ (1)

where v is the medium velocity, and h is the half-offset between the source and the receiver.

Additionally, by following simple trigonometry, we can connect the half-offset h with the depth of the reflection point z, as follows:  

$$h = \frac{z}{2}\, \frac{\sin{2\,\gamma}}{2\,\cos(\alpha+\g... ...\sin{\gamma}\,\cos{\gamma}}{\cos^2{\alpha} - \sin^2{\gamma}}\;.$$ (2)

Finally, the horizontal distance between the midpoint x and the reflection point $\xi$ is  

$$x - \xi = h\,\frac{\cos(\alpha-\gamma)\,\sin(\alpha+\gamma)... ...\,\frac{\sin{\alpha}\,\cos{\alpha}}{\sin{\gamma}\,\cos{\gamma}}$$ (3)

Equations (1-3) completely define the kinematics of angle-gather migration. Regrouping the terms, we can rewrite the three equations in a more symmetric form:

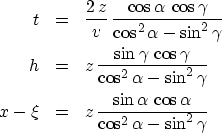$$\begin{eqnarray} t & = & \frac{2\,z}{v}\, \frac{\cos{\alpha}\,\cos{\gamma}}{\c... ...\frac{\sin{\alpha}\,\cos{\alpha}}{\cos^2{\alpha} - \sin^2{\gamma}}\end{eqnarray}$$ (4) (5) (6)

For completeness, here is the inverse transformation from t, h, and $x-\xi$ to z, $\gamma$, and $\alpha$:

$$\begin{eqnarray} z^2 & = & \frac{ \left[(v\,t/2)^2 - (x-\xi)^2\right]\, \le... ...left[(v\,t/2)^2 - (x-\xi)^2\right]} {(v\,t/2)^4 - h^2\,(x-\xi)^2}\end{eqnarray}$$ (7) (8) (9)

The inverse transformation (7-9) can be found by formally solving system (4-6).

The lines of constant reflection angle $\gamma$ and variable dip angle $\alpha$ for a given position of a reflection (diffraction) point $\{z,\xi\}$ have the meaning of summation curves for angle-gather Kirchhoff migration. The whole range of such curves for all possible values of $\gamma$ covers the diffraction traveltime surface - ``Cheops' pyramid'' Claerbout (1985) in the $\{t,x,h\}$space of seismic reflection data. As pointed out by Fowler (1997), this condition is sufficient for proving the kinematic validity of the angle-gather approach. For comparison, Figure 2 shows the diffraction traveltime pyramid from a diffractor at 0.5 km depth. The pyramid is composed of common-offset summation curves of the conventional time migration. Figure 3 shows the same pyramid composed of constant-$\gamma$ curves of the angle-gather migration.

 

coffset Figure 2 Traveltime pyramid, composed of common-offset summation curves.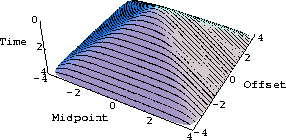

 

cangle Figure 3 Traveltime pyramid, composed of common-reflection-angle summation curves.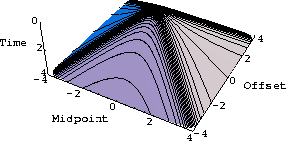

The most straightforward Kirchhoff algorithm of angle-gather migration can be formulated as follows:

• For each reflection angle $\gamma$ and each dip angle $\alpha$,
  • For each output location $\{z,\xi\}$,

    1.

    Find the traveltime t, half-offset h, and midpoint x from formulas (4), (5), and (6) respectively.

    2.

    Stack the input data values into the output.

As follows from equations (4-6), the range of possible $\alpha$'s should satisfy the condition  

$$\cos^2{\alpha} \gt \sin^2{\gamma}\quad\mbox{or}\quad \vert\alpha\vert + \vert\gamma\vert < \frac{\pi}{2}\;.$$ (10)

The described algorithm is not the most optimal in terms of the input/output organization, but it can serve as a basic implementation of the angle-gather idea. The stacking step requires an appropriate weighting. We discuss the weighting issues in the next section.