




Next: conclusion
Up: Guitton: Huber solver
Previous: L-BFGS update
The Huber norm Huber (1973, 1981) is a hybrid l1-l2 measure.
We expect to find the minimum of the function using a
quasi-Newton method with a L-BFGS update of the Hessian Guitton and Symes (1999). The Huber norm is
| 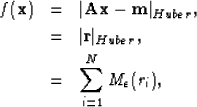 |
|
| (12) |
| |
where
 commands the limit between an l1 or l2 treatment of the residual; we call it
the Huber threshold and it must be given by the user. The gradient of the objective function
is given by
commands the limit between an l1 or l2 treatment of the residual; we call it
the Huber threshold and it must be given by the user. The gradient of the objective function
is given by
| 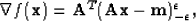 |
(14) |
where 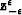 is the vector whose ith component is
is the vector whose ith component is
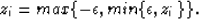
Because the Huber function is not twice continuously differentiable, it does not satisfy the three necessary
conditions that guarantee the convergence to a minimum. However, we only need to compute the gradient for
the BFGS update of the Hessian. Furthermore, given that the approximated Hessian is certainly a vague
approximation of the real one (Symes, 1999, Personal communication), the violation of the initial conditions is mild.
In addition, results Guitton (2000) show that this method converges to a minimum.
Li (1995) shows that the Huber function has a unique minimizer for any meaningful choice of  .
Indeed, if the l1 problem
.
Indeed, if the l1 problem 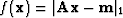 has multiple solutions Tarantola (1987),
then the Huber problem, provided that
has multiple solutions Tarantola (1987),
then the Huber problem, provided that  is small enough, also has multiple solutions. This is
annoying since we want to find a global minimum for the problem using quasi-Newton updates.
In practice, however, it seems that
is small enough, also has multiple solutions. This is
annoying since we want to find a global minimum for the problem using quasi-Newton updates.
In practice, however, it seems that
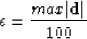
is a good choice for the threshold Darche (1989).
The threshold being set properly, the Huber function has mathematical properties
that allow the use of quasi-Newton methods. We can now define an efficient algorithm in order to
solve the Huber problem:
Algorithm2
- 1.
- Choose
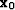 and the threshold
and the threshold  . Set k=0
. Set k=0
- 2.
- Compute
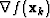 using equation 14
using equation 14
- 3.
- Compute
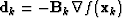 using a L-BFGS update (Algorithm 1, step 3)
using a L-BFGS update (Algorithm 1, step 3)
- 4.
- Compute the step
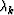 using a MoreThuente line search (
using a MoreThuente line search (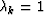 tried first)
tried first)
- 5.
- Update the solution
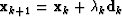
- 6.
- Go to step 2
This algorithm will converge to the minimizer 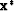 , as proven by Liu and Nocedal (1989).
, as proven by Liu and Nocedal (1989).





Next: conclusion
Up: Guitton: Huber solver
Previous: L-BFGS update
Stanford Exploration Project
4/27/2000
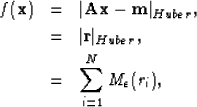
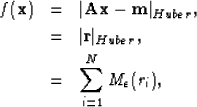
![]()
![]()