




Next: Filter estimation
Up: METHODOLOGY
Previous: METHODOLOGY
Consider
the recorded data 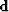 to be the simple superposition of ``signal''
to be the simple superposition of ``signal''  , i.e., reflection
events, and ``noise''
, i.e., reflection
events, and ``noise'' 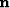 , i.e., multiples:
, i.e., multiples: 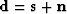 . For the special case of uncorrelated signal and noise, the so-called Wiener estimator
is a filter, which when applied to the data, yields an optimal (least-squares sense)
estimate of the embedded signal Castleman (1996). The frequency response
. For the special case of uncorrelated signal and noise, the so-called Wiener estimator
is a filter, which when applied to the data, yields an optimal (least-squares sense)
estimate of the embedded signal Castleman (1996). The frequency response
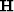 of this filter is
of this filter is
| 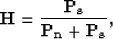 |
(1) |
where 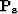 and
and 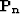 are the signal and noise power spectra, respectively.
Abma (1995) and Claerbout (1999) solved a constrained least squares problem
to separate signal from spatially uncorrelated noise:
are the signal and noise power spectra, respectively.
Abma (1995) and Claerbout (1999) solved a constrained least squares problem
to separate signal from spatially uncorrelated noise:
| 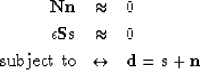 |
|
| (2) |
| |
where the operators 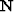 and
and 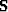 represent t-x domain convolution with
non-stationary PEF which whiten the unknown noise
represent t-x domain convolution with
non-stationary PEF which whiten the unknown noise 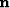 and
signal
and
signal  , respectively,
and
, respectively,
and  is a Lagrange multiplier. Minimizing
the quadratic
objective function suggested by equation (2) with respect to
is a Lagrange multiplier. Minimizing
the quadratic
objective function suggested by equation (2) with respect to  leads to the
following expression for the estimated signal:
leads to the
following expression for the estimated signal:
| 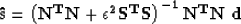 |
(3) |
By construction, the frequency response of a PEF approximates the inverse power spectrum of
the data from which it was estimated.
Thus, we see that the approach of equation (2) is similar to the Wiener reconstruction
process.
Spitz (1999) showed that for uncorrelated signal and noise, the
signal
can be expressed in terms of a PEF, 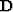 , estimated from the data
, estimated from the data
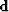 , and a PEF,
, and a PEF,
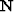 , estimated from the noise model:
, estimated from the noise model:
| 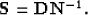 |
(4) |
Spitz' result applies to one-dimensional PEF's in the f-x domain, but our use
of the helix transform Claerbout (1998) permits stable inverse filtering
with multidimensional t-x domain filters.
Substituting 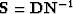 and applying the constraint
and applying the constraint 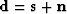 to equation (2) gives
to equation (2) gives
| 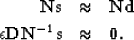 |
|
| (5) |
Iterative solutions to least-squares problems converge faster if the data and the model
being estimated are both uncorrelated. To precondition this problem, we again
appeal to
the Helix transform to make the change of variables 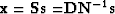 or
or 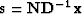 and apply it to equation (5):
and apply it to equation (5):
| 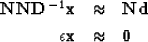 |
|
| (6) |
After solving equation (6) for the preconditioned solution  , we obtain
the estimated signal by reversing the change of variables:
, we obtain
the estimated signal by reversing the change of variables:
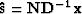 .
.





Next: Filter estimation
Up: METHODOLOGY
Previous: METHODOLOGY
Stanford Exploration Project
4/27/2000
![]() to be the simple superposition of ``signal''
to be the simple superposition of ``signal'' ![]() , i.e., reflection
events, and ``noise''
, i.e., reflection
events, and ``noise'' ![]() , i.e., multiples:
, i.e., multiples: ![]() . For the special case of uncorrelated signal and noise, the so-called Wiener estimator
is a filter, which when applied to the data, yields an optimal (least-squares sense)
estimate of the embedded signal Castleman (1996). The frequency response
. For the special case of uncorrelated signal and noise, the so-called Wiener estimator
is a filter, which when applied to the data, yields an optimal (least-squares sense)
estimate of the embedded signal Castleman (1996). The frequency response
![]() of this filter is
of this filter is
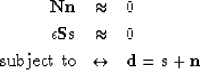
![]() , estimated from the data
, estimated from the data
![]() , and a PEF,
, and a PEF,
![]() , estimated from the noise model:
, estimated from the noise model:
![]() and applying the constraint
and applying the constraint ![]() to equation (2) gives
to equation (2) gives