Background

In general, geophysical inverse problems (inverting for some model ($\bf m$), given some ($\bf d$), while applying some operator ($\bf L$)) are ill-posed. A classic example of this is the missing data problem Claerbout (1999). The goal of the missing data problem is to interpolate intelligently between a sparse set of known points. For example, let's take a synthetic velocity model with an upper horizontal reflector, an anticline between two unconformities, and updipping layer at the bottom of the model. Suppose we have velocity measurements at several wells (Figure 1) and you would like to interpolate it onto a regular 2-D mesh.

 

well-logs
Figure 1 Left panel shows a synthetic velocity model, right panel shows a subset of that data chosen to simulate well log data.

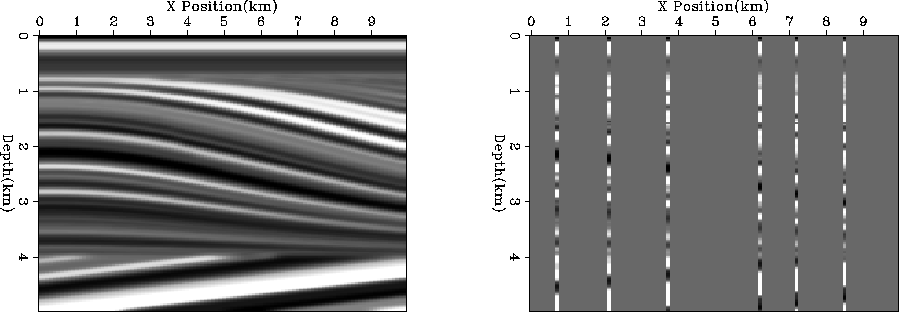The geophysicist might follow the approach described by Claerbout (1999), first interpolating the irregular data onto a regular mesh by applying some type of binning operator, $\bf B$,then defining a fitting goal that requires the model to fit the data exactly at the known points ($\bold J$),  

$${\bf J} {\bf B} \bf d\approx{\bf J} \bf m .$$ (1)

At model locations where there are no data values, we want the model to be `smooth', therefore we will use Tikhonov regularization to minimize the output of a roughening operator applied to the model,  

$$\bf 0\approx \bf A\bf m.$$ (2)

If we don't have any other knowledge about our model, an isotropic operator like the Laplacian might be a logical choice for $\bf A$since it leads to the ``minimum energy'' solution. If I apply the fitting goals implied by (1) and (2) for 200 iterations using the Laplacian for $\bf A$ I get Figure 2. The result is what has been euphemistically referred to as the `ice cream cone result' Brown (1998). By spreading information isotropically, the model goes smoothly from our known points to some local average. We see little to no continuation of layers, which is generally a thoroughly unsatisfactory result.

 

qdome-lap Figure 2 Interpolation result after 200 iterations using an inverse Laplacian regularization operator. Note the edges effects at the top and bottom of the model due to using a internal convolution operator.