




Next: Synthetic 1
Up: Rosales: Velocity
Previous: Problems involved
A basic daily problems in seismic
processing, such as the estimation of interval velocities from RMS
velocities, will be solved in this part.
The method used here was first introduced by Clapp et al. (1998). The
method builds a velocity model from surface seismology while retaining
the null-space. They start from fundamental concepts in Geophysical
Estimation by Example Claerbout (1997)
and define the simplest interval velocity estimation including the
notion of null-space. Generally, Clapp et al. (1998)
minimize interval velocities ``wiggliness'' where there are not
good quality reflections.
In order to understand the method
used in this part it is necessary to make some definitions
(for further explanation the reader could refer to Clapp et al. (1998):
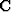
- as the matrix of causal integration, a lower triangular matrix of ones.
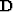
- as the matrix of causal differentiation, namely,
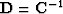 .
. 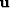
- as a vector whose components range over the vertical
traveltime depth
 ,and whose component values contain the interval velocity squared
,and whose component values contain the interval velocity squared
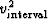 .
. 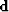
- as a data vector whose components range over the vertical
travel time depth
 ,and whose component values contain the scaled RMS velocity squared
,and whose component values contain the scaled RMS velocity squared
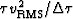 where
where
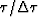 is the index on the time axis.
is the index on the time axis.
The theoretical (squared) RMS velocity is defined by
| 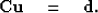 |
(1) |
With imperfect data, our data fitting goal is to minimize the
residual
| ![\begin{displaymath}
\bold 0
\quad\approx\quad
\bold W
\left[
\bold C\bold u
-
\bold d
\right] .\end{displaymath}](img15.gif) |
(2) |
To find the interval velocity where there is no data, we have the ``model damping'' goal to
minimize the ``wiggliness'' 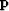 of the squared interval velocity
of the squared interval velocity 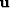
| 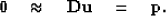 |
(3) |
These two goals are preconditioned by changing the optimization variable from interval velocity
squared 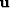 to its wiggliness
to its wiggliness 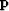 . Substituting
. Substituting 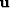 =
= 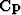 gives the
two fitting goals expressed as a function of wiggliness
gives the
two fitting goals expressed as a function of wiggliness 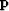
| ![\begin{eqnarray}
\bold 0
&\approx&
\bold W'
\left[
\bold C^2\bold p
-
\bold d
\right]
\\ \bold 0
&\approx&
\epsilon \bold p .\end{eqnarray}](img19.gif) |
(4) |
| (5) |
This method was tested on two synthetic CMP gathers and one
real CMP gather from the Gulf of Mexico.





Next: Synthetic 1
Up: Rosales: Velocity
Previous: Problems involved
Stanford Exploration Project
4/27/2000
![]() of the squared interval velocity
of the squared interval velocity ![]()