




Next: Shaping filers on a
Up: Theory
Previous: Cross-correlation and shaping filters
The first step is to consider non-stationary shaping filters.
Experience with missing data problems
Crawley et al. (1998); Crawley (1999b) has shown that
working with smoothly-varying non-stationary filters often gives
better results than working with filters that are stationary within
small patches.
With a non-stationary convolution filter, 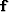 , the shaping
filter regression equations,
, the shaping
filter regression equations,
| 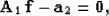 |
(3) |
are massively underdetermined since there is a potentially unique
impulse response associated with every point in the dataspace
Rickett (1999). We need constraints to ensure the
filters vary-smoothly in some manner.
The simplest regularization scheme involves applying a generic
data-space roughening operator, 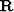 , to the non-stationary
filter coefficients.
, to the non-stationary
filter coefficients. 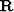 can be a simple derivative operator,
for example. This leads to the set of equations,
can be a simple derivative operator,
for example. This leads to the set of equations,
| 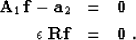 |
(4) |
| (5) |
By making the change of variables,
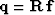 Fomel (1997b),
we get the following system of equations,
Fomel (1997b),
we get the following system of equations,
| 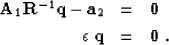 |
(6) |
| (7) |
Equations (6) and (7) describe a
preconditioned linear system of equations, the solution to which
converges rapidly under an iterative conjugate-gradients solver.
In practice, I set 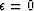 , and keep the filters smooth by
restricting the number of iterations Crawley (1999a).
, and keep the filters smooth by
restricting the number of iterations Crawley (1999a).





Next: Shaping filers on a
Up: Theory
Previous: Cross-correlation and shaping filters
Stanford Exploration Project
4/27/2000
![]() , the shaping
filter regression equations,
, the shaping
filter regression equations,
![]() , to the non-stationary
filter coefficients.
, to the non-stationary
filter coefficients. ![]() can be a simple derivative operator,
for example. This leads to the set of equations,
can be a simple derivative operator,
for example. This leads to the set of equations,