




Next: methodology
Up: Brown & Claerbout: Radial
Previous: Brown & Claerbout: Radial
The Radial Trace Transform (RTT), is a simple coordinate transform of normal
(t,x) domain seismic gathers; a horizontal deformation, accomplished by the
following linear mapping
| 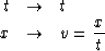 |
(1) |
| |
The radial coordinate is termed ``v'' because the RTT sorts the data by apparent
velocity. Neglecting dispersion effects, ground roll maps to zero temporal frequency
in the RT domain.
The RTT is not a new concept. Nearly twenty years ago, this coordinate transform
was an active subject of research for use in multiple suppression Taner (1980),
migration Ottolini (1982), and even for the subject of this paper, ground roll removal
Claerbout (1983). Henley's 1999 recent paper reminded the
world of the RTT's usefulness in attacking ground roll. Sava and Fomel (2000) use
the RTT to compute angle gathers, exploiting the fact that slant-stack in the (t,x) domain
is equivalent to computing the RTT in the Fourier domain.
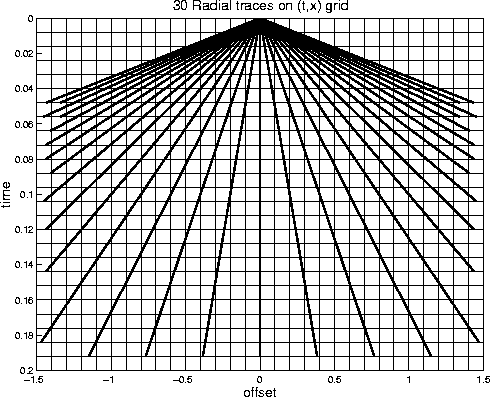
Figure 1 shows 30 radial traces (thick lines) overlain on a rectangular
(t,x) mesh. Points along radial traces rarely fall exactly on (t,x) data locations,
making the RTT an exercise in interpolation. In matrix notation, let us denote the RTT
of data 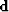 as follows:
as follows:
| 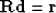 |
(2) |
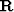 is generally non-square, and even if square, is usually noninvertible. Often,
however, such interpolation operators are nearly unitary:
is generally non-square, and even if square, is usually noninvertible. Often,
however, such interpolation operators are nearly unitary: 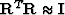 .
We define the interpolation error as follows
.
We define the interpolation error as follows
| ![\begin{displaymath}
\bf e = \left[\bold I - {\bf R}^T \bf R \right] d.\end{displaymath}](img6.gif) |
(3) |
figure1
Figure 1 30 radial traces overlaying a (t,x) grid.
|
|  |






Next: methodology
Up: Brown & Claerbout: Radial
Previous: Brown & Claerbout: Radial
Stanford Exploration Project
4/28/2000
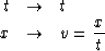
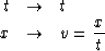
![]() as follows:
as follows:
