Examples

We exemplify the proposed method on two synthetic models and two real datasets.

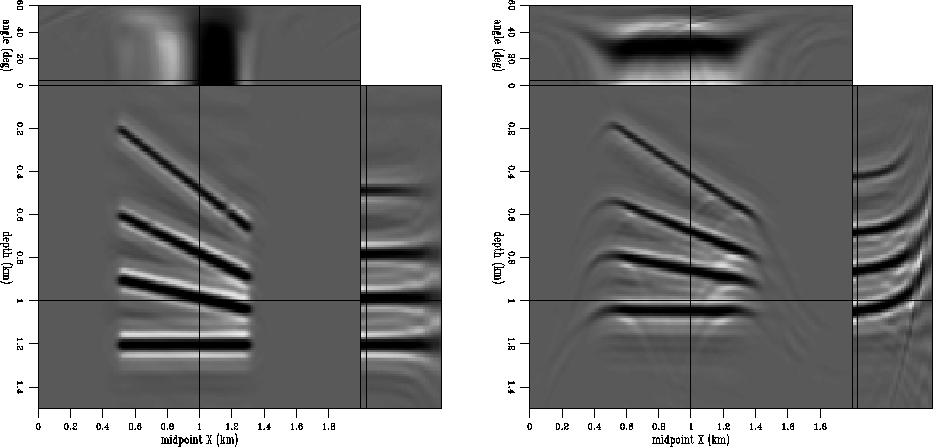
The first example is a 2-D synthetic model with dipping reflectors at various angles. We generated the synthetic data using wave-equation modeling Biondi (1999). Next, we imaged the data, first using the correct and then using an incorrect velocity model, a slower velocity in this example. In the case of correct velocity, the ADCIGs are flat, but they are not flat in the case of the incorrect velocity model (Figure 2). Because the simulated acquisition is represented by wide offsets and the model is reasonably shallow, there is no significant decrease in the angular coverage at the deeper reflectors. However, the steep reflectors are characterized by smaller angular coverage due to the limited acquisition geometry.

 

dipsynt.cig01
Figure 2 The first synthetic model. The reflectivity is composed of interfaces dipping at different angles. All the events are flat along the reflection angle axis, in the case where we use the correct velocity (left). However, when we use a wrong velocity model, the image loses focus and the ADCIGs bend (right).

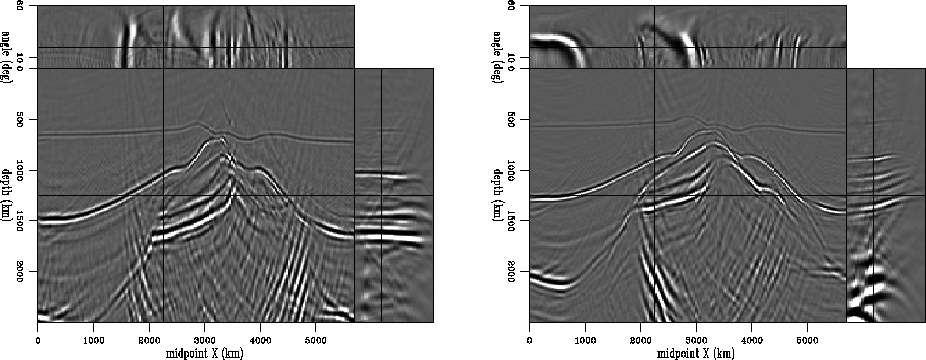
In the second example, we consider a more complex synthetic model, centered on a salt body. The model was generated at Elf-IFP-CGG and inspired by real data recorded in the North Sea Prucha et al. (1998). Again, we image both with a correct velocity model and an incorrect one (Figure3). The conclusions are similar to those in the first example: correct velocity flattens the events in the angle-domain common-image gathers, while incorrect velocity does not. Again, there is no significant decrease in the angular coverage at the deeper reflector.

 

saltsynt.cig01
Figure 3 The second synthetic model, depicting a salt body. The ADCIGs show flat events when the velocity model is correct (left), but bend when the velocity is incorrect.

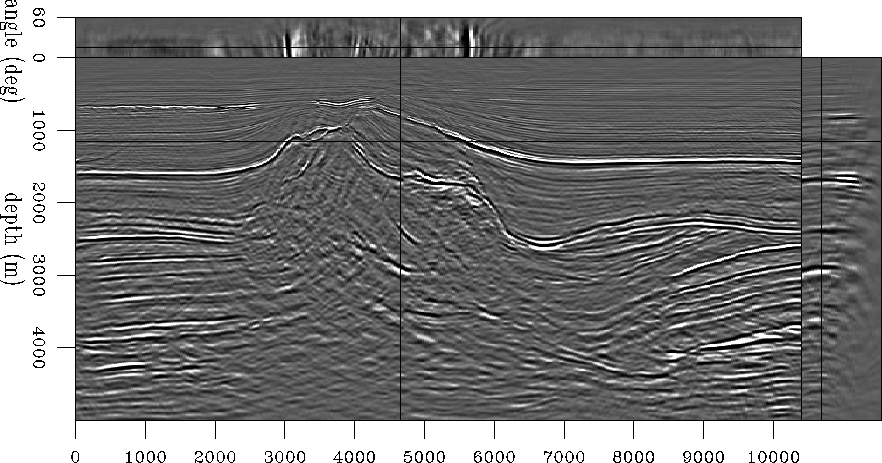
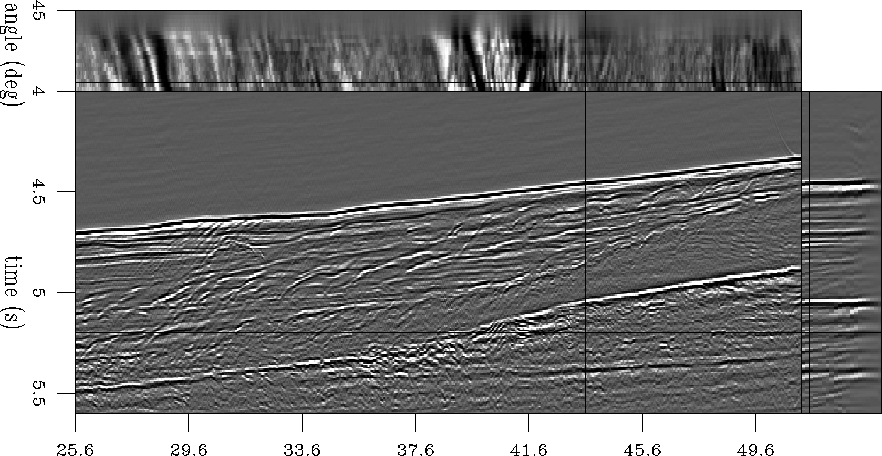
The third example is a real dataset acquired in a salt-dome region of the North Sea Prucha et al. (1998); Vaillant and Sava (1999). Figure 4 depicts a slice of the image taken at a small reflection angle, and the small panels at the top and the right represent ADCIGs. The image generated for this dataset goes much deeper compared to the preceding synthetics, and we see that the angular coverage decreases as the depth increases. Some of the events appear flat, while others are bending, indicating velocity inaccuracies.

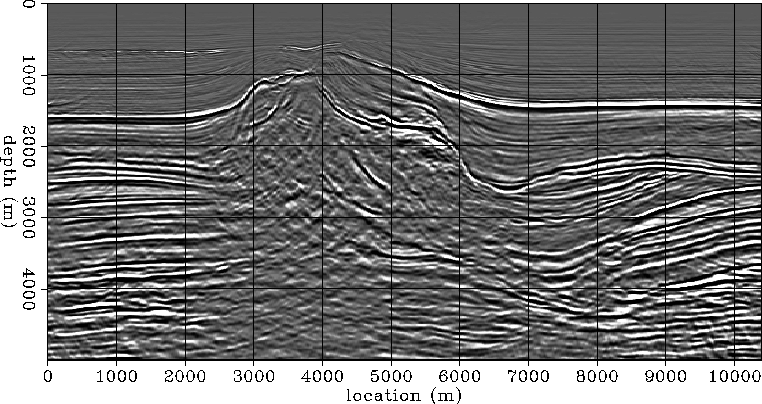
It is apparent from the image that some of the events lose their sharpness and the relative contrast decreases. This is understandable, since the energy of every event is spread along the angle axis. The true migrated image could be recovered by summation along the angle axis (Figure 5).

 

saltreal.cig
Figure 4 Migrated image for the North Sea dataset presented as ADCIGs. The ADCIGs are mostly flat, but they reveal the areas where the velocity map needs improvement. The image as a whole loses part of its sharpness, because the energy of each event is spread along the angle axis.

 

saltreal.stk
Figure 5 Migrated image for the North Sea dataset, stacked over the angle axis in the ADCIGs.

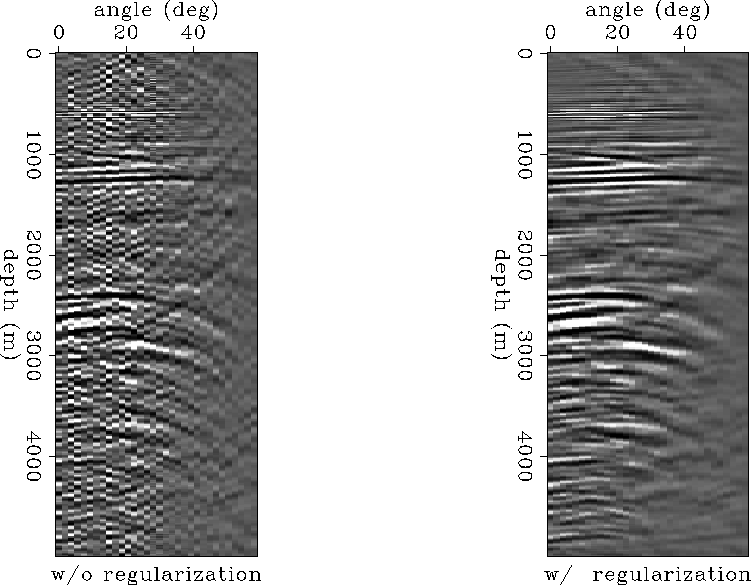
This example enables us to analyze the efficiency of our regularization method. Figure 6 shows angle-domain common-image gathers for a particular midpoint. The left panel represents the result obtained without regularization ($\epsilon=0.0$). In contrast, the panel on the right shows the result we obtain with regularization ($\epsilon=1.0$). The regularized image is much cleaner, without visible distortions of the shape and amplitudes of the events. Since the noise level is much lower, we can easily identify faint events that would otherwise be impossible to discern, for example at depths greater than 4000 m.

 

saltreal.eps Figure 6 A comparison of ADCIGs with regularization (right panel) and without regularization (left panel).

Finally, a fourth example addresses the amplitude variation with angle analysis (AVA) issue. Our method produces the output as a function of the reflection angle, which makes it an ideal tool for AVA analysis. The crucial question is how much the amplitudes are affected by the method, especially given that we impose a certain amount of smoothness through regularization. Previous research Prucha et al. (1999a) indicates that ADCIGs obtained by wave-equation imaging have the potential to preserve AVA effects.

For the AVA example, we use a dataset from a gas-hydrates study, for which the AVO effects are significant Ecker (1998). Figure 7 represents the wave-equation migrated image, displayed as ADCIGs. Figure 8 shows 4 wiggle-plots of ADCIGs located around 45 km from the left origin of the survey. This area is particularly interesting since it captures both the bottom-simulation reflector (BSR) and the flat reflector from the hydrate-gas transition. The results confirm the amplitude trend variation previously highlighted for this dataset; specifically, we can observe significant amplitude increase as a function of angle, especially for the BSR. This result was obtained for a moderate choice of the regularization parameter (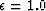$\epsilon=1.0$). Caution should be exercised in this matter, since a higher value could attenuate the amplitude of the variations. A more thorough and quantitative analysis awaits future research.

It is worth mentioning that, in certain applications, the amplitude variations with angle are undesirable. A good example is velocity-analysis where AVA effects can be misleading and indicate incorrect updates of the velocity model. However, we can perhaps control this by boosting the $\epsilon$ parameter, with the effect of attenuating the variations along angles.

 

hydrreal.cig
Figure 7 Migrated image for the gas-hydrates data presented as ADCIGs.