




Next: Tests
Up: Fomel: Offset continuation
Previous: Introduction
If 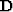 is a regularization operator, and
is a regularization operator, and 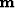 is the
estimated model, then Claerbout's interpolation method amounts to
minimizing the power of
is the
estimated model, then Claerbout's interpolation method amounts to
minimizing the power of 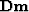 (
(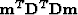 ) under the constraint
) under the constraint
|  |
(1) |
where  stands for the known data values, and
stands for the known data values, and  is
a diagonal matrix with 1s at the known data locations and zeros
elsewhere. It is easy to implement a constraint of the
form (1) in an iterative conjugate-gradient scheme by
simply disallowing the iterative process to update model parameters at
the known data locations Claerbout (1999).
is
a diagonal matrix with 1s at the known data locations and zeros
elsewhere. It is easy to implement a constraint of the
form (1) in an iterative conjugate-gradient scheme by
simply disallowing the iterative process to update model parameters at
the known data locations Claerbout (1999).
The operator  can be considered as a differential equation
that we assume the model to satisfy. If
can be considered as a differential equation
that we assume the model to satisfy. If 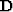 is able to remove
all correlated components from the model and produce white Gaussian
noise in the output, then
is able to remove
all correlated components from the model and produce white Gaussian
noise in the output, then 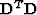 is essentially
equivalent to the inverse covariance matrix of the model, which
appears in the statistical formulation of least-squares estimation
Tarantola (1987).
is essentially
equivalent to the inverse covariance matrix of the model, which
appears in the statistical formulation of least-squares estimation
Tarantola (1987).
In this paper, I propose to use the offset continuation equation
Fomel (1995a) for the operator 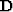 . Under certain
assumptions, this equation is indeed the one that prestack seismic
reflection data can be presumed to satisfy. The equation has the
following form:
. Under certain
assumptions, this equation is indeed the one that prestack seismic
reflection data can be presumed to satisfy. The equation has the
following form:
| 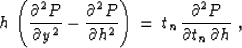 |
(2) |
where P(tn,h,x) is the prestack seismic data after the normal
moveout correction (NMO), tn stands for the time coordinate after
NMO, h is the half-offset, and y is the midpoint. Offset
continuation has the following properties:
- Equation (2) describes an artificial process
of prestack data transformation in the offset direction. It belongs
to the class of linear hyperbolic equations. Therefore, the
described process is a wave-type process. Half-offset h serves as
a continuation variable (analogous to time in the wave equation).
- Under a constant-velocity assumption,
equation (2) provides correct reflection
traveltimes and amplitudes at the continued sections. The amplitudes
are correct in the sense that the geometrical spreading effects are
properly transformed independently from the shape of the reflector.
This fact has been confirmed both by the ray method approach
Fomel (1995a) and by the Kirchhoff modeling approach
Fomel et al. (1996); Fomel and Bleistein (1996).
- Dip moveout (DMO) Hale (1995) can be regarded as a particular
case of offset continuation to zero offset
Deregowski and Rocca (1981). As shown in my earlier paper
Fomel (1995b), different known forms of DMO operators can
be obtained as solutions of a special initial-value problem on
equation (2).
- To describe offset continuation for 3-D data, we need a pair of
equations such as (2), acting in two orthogonal
projections. This fact follows from the analysis of the azimuth
moveout operator Biondi et al. (1998); Fomel and Biondi (1995).
- A particularly efficient implementation of offset continuation
results from a log-stretch transform of the time coordinate
Bolondi et al. (1982), followed by a Fourier transform of the
stretched time axis. After these transforms,
equation (2) takes the form
| 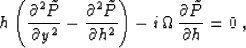 |
(3) |
where 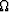 is the corresponding frequency, and
is the corresponding frequency, and 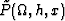 is the transformed data Fomel (1995b). As in
other F-X methods, equation (3) can be applied
independently and in parallel on different frequency slices.
is the transformed data Fomel (1995b). As in
other F-X methods, equation (3) can be applied
independently and in parallel on different frequency slices.
I propose to adopt a finite-difference form of the differential
operator (3) for the regularization operator 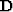 . A
simple analysis of equation (3) shows that at small
frequencies, the operator is dominated by the first term. The form
. A
simple analysis of equation (3) shows that at small
frequencies, the operator is dominated by the first term. The form
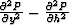 is equivalent to the second mixed derivative in the source and
receiver coordinates. Therefore, at low frequencies, the offset waves
propagate in the source and receiver directions. At high frequencies,
the second term in (3) becomes dominating, and the entire
method becomes equivalent to the trivial linear interpolation in
offset. The interpolation pattern is more complicated at intermediate
frequencies.
is equivalent to the second mixed derivative in the source and
receiver coordinates. Therefore, at low frequencies, the offset waves
propagate in the source and receiver directions. At high frequencies,
the second term in (3) becomes dominating, and the entire
method becomes equivalent to the trivial linear interpolation in
offset. The interpolation pattern is more complicated at intermediate
frequencies.





Next: Tests
Up: Fomel: Offset continuation
Previous: Introduction
Stanford Exploration Project
4/28/2000
![]() is a regularization operator, and
is a regularization operator, and ![]() is the
estimated model, then Claerbout's interpolation method amounts to
minimizing the power of
is the
estimated model, then Claerbout's interpolation method amounts to
minimizing the power of ![]() (
(![]() ) under the constraint
) under the constraint
![]() can be considered as a differential equation
that we assume the model to satisfy. If
can be considered as a differential equation
that we assume the model to satisfy. If ![]() is able to remove
all correlated components from the model and produce white Gaussian
noise in the output, then
is able to remove
all correlated components from the model and produce white Gaussian
noise in the output, then ![]() is essentially
equivalent to the inverse covariance matrix of the model, which
appears in the statistical formulation of least-squares estimation
Tarantola (1987).
is essentially
equivalent to the inverse covariance matrix of the model, which
appears in the statistical formulation of least-squares estimation
Tarantola (1987).
![]() . Under certain
assumptions, this equation is indeed the one that prestack seismic
reflection data can be presumed to satisfy. The equation has the
following form:
. Under certain
assumptions, this equation is indeed the one that prestack seismic
reflection data can be presumed to satisfy. The equation has the
following form:
![]() . A
simple analysis of equation (3) shows that at small
frequencies, the operator is dominated by the first term. The form
. A
simple analysis of equation (3) shows that at small
frequencies, the operator is dominated by the first term. The form
![]() is equivalent to the second mixed derivative in the source and
receiver coordinates. Therefore, at low frequencies, the offset waves
propagate in the source and receiver directions. At high frequencies,
the second term in (3) becomes dominating, and the entire
method becomes equivalent to the trivial linear interpolation in
offset. The interpolation pattern is more complicated at intermediate
frequencies.
is equivalent to the second mixed derivative in the source and
receiver coordinates. Therefore, at low frequencies, the offset waves
propagate in the source and receiver directions. At high frequencies,
the second term in (3) becomes dominating, and the entire
method becomes equivalent to the trivial linear interpolation in
offset. The interpolation pattern is more complicated at intermediate
frequencies.