




Next: Why two methods?
Up: Introduction
Previous: Introduction
The two proposed methods are based on the need to
have IID residual components. A typical inverse problem arises when we want
to minimize the objective function for the fitting goal
| 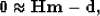 |
(2) |
where  is a mapping of the data (unknown of the inverse problem),
is a mapping of the data (unknown of the inverse problem),  an operator
and
an operator
and  the seismic data. The residual r is defined as the difference between input
data d and estimated data
the seismic data. The residual r is defined as the difference between input
data d and estimated data 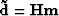 ,
My research is focused on the attenuation/separation
of the coherent noise only.
The first strategy relates to fundamentals in inverse theory as
detailed in the General Discrete Inverse Problem Tarantola (1987) and
approximates the inverse covariance matrices with PEFs.
The second strategy proposes to introduce a coherent noise
modeling part in Equation 2. The noise operator will be a PEF.
In the first strategy the coherent noise is filtered.
In the second strategy the coherent noise is subtracted from the signal.
The two methods should (1) give IID residual components, (2) stabilize the inversion,
and (3) preserve the ``real'' events amplitudes as long as the noise and the signal
operators have been carefully chosen.
,
My research is focused on the attenuation/separation
of the coherent noise only.
The first strategy relates to fundamentals in inverse theory as
detailed in the General Discrete Inverse Problem Tarantola (1987) and
approximates the inverse covariance matrices with PEFs.
The second strategy proposes to introduce a coherent noise
modeling part in Equation 2. The noise operator will be a PEF.
In the first strategy the coherent noise is filtered.
In the second strategy the coherent noise is subtracted from the signal.
The two methods should (1) give IID residual components, (2) stabilize the inversion,
and (3) preserve the ``real'' events amplitudes as long as the noise and the signal
operators have been carefully chosen.





Next: Why two methods?
Up: Introduction
Previous: Introduction
Stanford Exploration Project
9/5/2000