




Next: Extension to 3-D
Up: Clapp: 3-D tomography field
Previous: Introduction
Following the methodology of Clapp and Biondi (1999a), I will
begin by considering a regularized tomography problem.
I will linearize around an initial slowness estimate and find
a linear operator in the vertical
traveltime domain 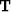 between our change in slowness
between our change in slowness 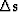 and our change in traveltimes
and our change in traveltimes 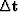 .We will write a set of fitting goals,
.We will write a set of fitting goals,
| 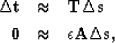 |
|
| (1) |
where 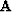 is our steering filter operator and
is our steering filter operator and  is a
Lagrange multiplier.
However, these
fitting goals don't accurately describe what
we really want. Our steering filters are based on our
desired slowness rather than change of slowness. With this
fact in mind, we can rewrite our second fitting goal as:
is a
Lagrange multiplier.
However, these
fitting goals don't accurately describe what
we really want. Our steering filters are based on our
desired slowness rather than change of slowness. With this
fact in mind, we can rewrite our second fitting goal as:
| 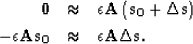 |
(2) |
| (3) |
Our second fitting goal can not be strictly defined as regularization
but we can do a preconditioning substitution Fomel et al. (1997),
giving us a new set of fitting goals:
| 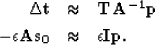 |
|
| (4) |





Next: Extension to 3-D
Up: Clapp: 3-D tomography field
Previous: Introduction
Stanford Exploration Project
9/5/2000