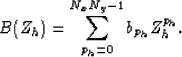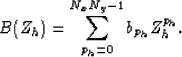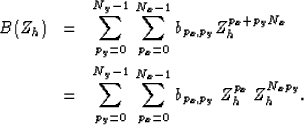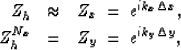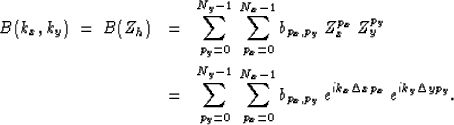Next: Wavenumber in helical coordinates
Up: Theory
Previous: Theory
Taking the one-dimensional Z transform of 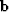 in the helical
coordinate system gives
in the helical
coordinate system gives
| 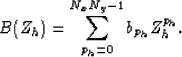 |
(1) |
Here, Zh represents the unit delay operator in the sampled
(helical) coordinate system.
The summation in equation (1) can be split into two
components,
| 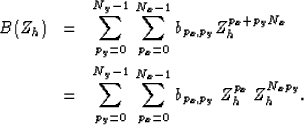 |
(2) |
| (3) |
Ignoring boundary effects, a single unit delay in the helical
coordinate system is equivalent to a single unit delay on the
x-axis;
similarly, but irrespective of boundary conditions, Nx unit delays
in the helical coordinate system are equivalent to a single delay on
the y-axis.
This leads to the following definitions of Zh and
ZhNx in terms of delay operators, Zx and Zy, or
wavenumbers, kx and ky:
| 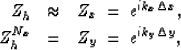 |
(4) |
| (5) |
where 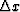 and
and 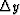 define the grid-spacings along the x
and y-axis respectively.
define the grid-spacings along the x
and y-axis respectively.
Substituting equations (4) and (5) into
equation (3) leaves
| 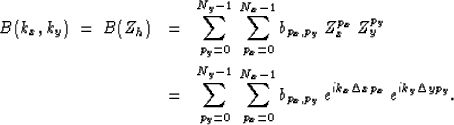 |
(6) |
| (7) |
Equation (7) implies that, if we ignore boundary
effects, the one-dimensional FFT of 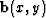 in helical
coordinates is equivalent to its two-dimensional Fourier transform.
in helical
coordinates is equivalent to its two-dimensional Fourier transform.





Next: Wavenumber in helical coordinates
Up: Theory
Previous: Theory
Stanford Exploration Project
9/5/2000