




Next: Regularization
Up: Brown: Sparse data interpolation
Previous: Introduction
Many types of geophysical data consist of measurements of a given quantity, collected at
arbitrary locations near the earth's surface.
The problem is to infer the value of this quantity at all locations in the study area -
in other words, to estimate the earth model of the quantity that gave rise to the collected data.
These ideas are embodied in the following simple linear relationship
| 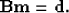 |
(1) |
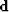 and
and 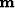 are the measured data and estimated model, respectively, while
are the measured data and estimated model, respectively, while 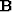 is a linear operator that carries out the ``experiment'' by sampling the model at the
measurement locations and mapping these values to the data vector. However, the reverse -
an estimate of the model, given the data - is usually more useful. In this case,
is a linear operator that carries out the ``experiment'' by sampling the model at the
measurement locations and mapping these values to the data vector. However, the reverse -
an estimate of the model, given the data - is usually more useful. In this case, 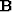 must
be ``inverted'' in some sense:
must
be ``inverted'' in some sense:
| 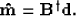 |
(2) |
The simplest choice is 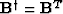 , but any choice so that the model
honors the known data has a measure of validity.
, but any choice so that the model
honors the known data has a measure of validity.
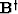 may also be cast as a least squares inverse. Depending on the acquisition
geometry of the experiment, the least squares problem may be underdetermined, overdetermined,
or more commonly, both Menke (1989).
For purely overdetermined problems, the least squares inverse is
may also be cast as a least squares inverse. Depending on the acquisition
geometry of the experiment, the least squares problem may be underdetermined, overdetermined,
or more commonly, both Menke (1989).
For purely overdetermined problems, the least squares inverse is
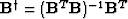 , but if some model points
are undetermined,
, but if some model points
are undetermined, 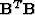 is singular.
is singular.





Next: Regularization
Up: Brown: Sparse data interpolation
Previous: Introduction
Stanford Exploration Project
9/5/2000