




Next: Multiscale regularization
Up: Background
Previous: Regularization
We can precondition equation (3) by making a simple change of variables:
| 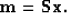 |
(5) |
Analogous to equation (4), we can write the least squares inverse for the
preconditioned model  :
:
| 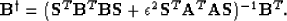 |
(6) |
If 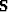 is the left inverse of
is the left inverse of 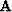 (
(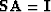 ), then equation (6)
reduces to the classic damped least squares problem Menke (1989):
), then equation (6)
reduces to the classic damped least squares problem Menke (1989):
| 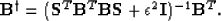 |
(7) |
If 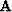 is a differential operator,
is a differential operator, 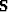 is then a smoothing operator, and it follows that
the smallest eigenvalues of
is then a smoothing operator, and it follows that
the smallest eigenvalues of 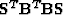 correspond to the
complex (high frequency) model components. In contrast to equation (4), smooth,
useful models will appear in early iterations of the preconditioned problem of equation
(7), although absolute rate of convergence to the same final result should not change.
correspond to the
complex (high frequency) model components. In contrast to equation (4), smooth,
useful models will appear in early iterations of the preconditioned problem of equation
(7), although absolute rate of convergence to the same final result should not change.
Spectral factorization Sava et al. (1998) and the Helix transform Claerbout (1998) permit
multidimensional, recursive,
approximate inverse filtering, so it is indeed possible to compute 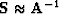 for many choices of
for many choices of 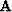 . One downside of recursive filter preconditioning is that the operator is
difficult to parallelize. For large problems, the cost of a single least squares iteration may be
considerable, so the parallelization issue should be kept in mind.
. One downside of recursive filter preconditioning is that the operator is
difficult to parallelize. For large problems, the cost of a single least squares iteration may be
considerable, so the parallelization issue should be kept in mind.





Next: Multiscale regularization
Up: Background
Previous: Regularization
Stanford Exploration Project
9/5/2000
![]() for many choices of
for many choices of ![]() . One downside of recursive filter preconditioning is that the operator is
difficult to parallelize. For large problems, the cost of a single least squares iteration may be
considerable, so the parallelization issue should be kept in mind.
. One downside of recursive filter preconditioning is that the operator is
difficult to parallelize. For large problems, the cost of a single least squares iteration may be
considerable, so the parallelization issue should be kept in mind.