




Next: Conclusions
Up: Application examples
Previous: Trace interpolation beyond aliasing
Signal and noise separation and noise attenuation are yet another
important application of plane-wave prediction filters
Abma (1995); Brown et al. (1999); Canales (1984); Claerbout and Fomel (2000); Clapp and Brown (2000); Soubaras (1995); Spitz (1999).
The problem has a very clear interpretation in terms of the local dip
components. If two components, 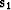 and
and 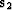 are
estimated from the data, and we can interpret the first component as
signal, and the second component as noise, then the signal and noise
separation problem reduces to solving the least-squares system
are
estimated from the data, and we can interpret the first component as
signal, and the second component as noise, then the signal and noise
separation problem reduces to solving the least-squares system
| 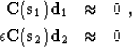 |
(19) |
| (20) |
for the unknown signal and noise components 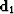 and
and
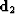 of the input data
of the input data 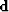 :
:
| 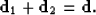 |
(21) |
The scalar parameter  in equation (20) reflects
the signal to noise ratio. We can combine equations (19-20)
and (21) in the explicit system for the
noise component
in equation (20) reflects
the signal to noise ratio. We can combine equations (19-20)
and (21) in the explicit system for the
noise component 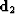 :
:
| 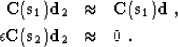 |
(22) |
| (23) |
Figure 17 shows a simple example of the described approach.
I estimated two dip components from the input synthetic data in a
manner similar to that of Figure 10, and separated the
corresponding events by solving the least-squares
system (22-23). The separation result is visually
perfect.
sn2
Figure 17 Simple example of dip-based single
and noise separation. From left to right: ideal signal, input data,
estimated signal, estimated noise.





Figure 18 presents a significantly more complicated
case: a receiver line from of a 3-D land shot gather from Saudi Arabia,
contaminated with three-dimensional hyperbolic ground-roll. The same
dataset has been used previously by Brown et al. (1999).
The ground-roll noise and the reflection events have a significantly
different frequency content, which might suggest an idea of separating
them on the base of frequency alone. The result of frequency-based
separation, shown in Figure 19 is, however, not ideal:
part of the noise remains in the estimated signal after the
separation. Changing the  parameter in
equation (23) could clean up the signal estimate, but it
would also bring some of the signal into the subtracted noise. A
better strategy is to separate the events by using both the difference
in frequency and the difference in slope. For that purpose, I adopted
the following algorithm:
parameter in
equation (23) could clean up the signal estimate, but it
would also bring some of the signal into the subtracted noise. A
better strategy is to separate the events by using both the difference
in frequency and the difference in slope. For that purpose, I adopted
the following algorithm:
- 1.
- Use a frequency-based separation (or, alternatively, a simple
low-pass filtering) to obtain an initial estimate of the ground-roll
noise.
- 2.
- Select a window around the initial noise. The further
separation will happen only in that window.
- 3.
- Estimate the noise dip from the initial noise estimate.
- 4.
- Estimate the signal dip in the selected data window as the
complimentary dip component to the already known noise dip.
- 5.
- Use the signal and noise dips together with the signal and noise
frequencies to perform the final separation. This is
achieved by cascading single-dip plane-wave destructor filters with
local 1-D three-coefficient PEFs, destructing a particular
frequency.
The separation result is shown in Figure 20. The
separation goal has been fully achieved: the estimated ground-roll noise is
free of the signal components, and the estimated signal is free of the
noise.
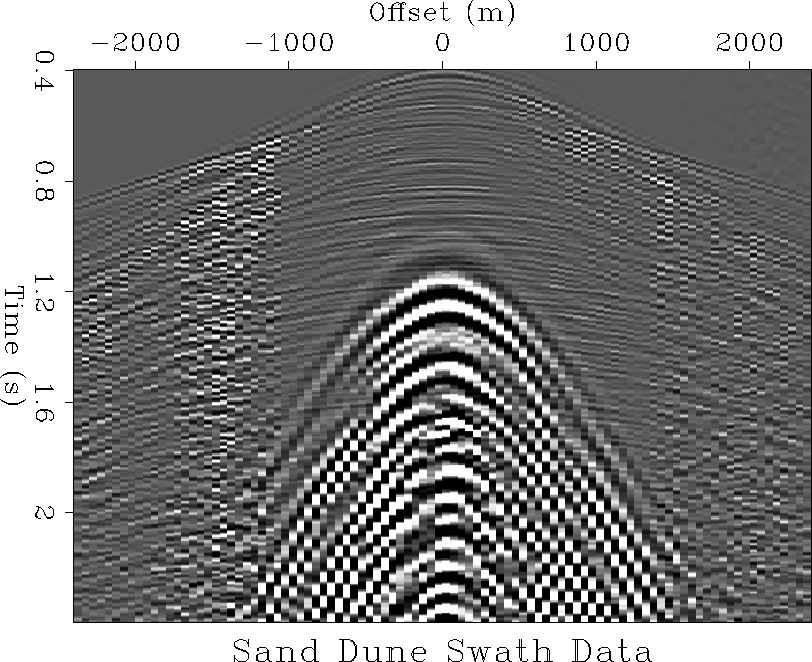
dune-dat
Figure 18 Ground-roll-contaminated data
from Saudi Arabian sand dunes. A slice out of a 3-D shot gather.




 dune-exp
dune-exp
Figure 19 Signal and noise separation
based on frequency. Top: estimated signal. Bottom: estimated noise.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)




 dune-sn
dune-sn
Figure 20 Signal and noise separation based
on both dip and frequency. Top: estimated signal. Bottom: estimated
noise.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





The left plot in Figure 21 shows another test example:
a shot gather contaminated by nearly linear low-velocity noise. In
this case, a simple dip-based separation was sufficient for achieving
a good result. The algorithm proceeds as follows
- 1.
- Bandpass the original data with an appropriate low-pass filter
to obtain an initial noise estimate (the right plot in
Figure 21.)
- 2.
- Estimate the local noise dip from the initial noise model.
- 3.
- Estimate the signal dip from the input data as the complimentary
dip component to the already known noise dip.
- 4.
- Estimate the noise by an iterative optimization of
system (22-23) and subtract it from the data to
get the signal estimate.
Figure 22 shows the separation result. The signal and noise
components are nicely separated. Guitton (2000) uses
the same data example to develop a method of pairing noise separation
with stacking velocity analysis.
ant-dat
Figure 21 Left: Input noise-contaminated
shot gather. Right: Result of low-pass filtering.




 ant-sn
ant-sn
Figure 22 Signal and noise separation
based on dip. Left: estimated signal. Right: estimated noise.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





The examples in this subsection show that when the signal and noise
components have distinctly different local slopes, we can
successfully separate them with plane-wave destructor filters.





Next: Conclusions
Up: Application examples
Previous: Trace interpolation beyond aliasing
Stanford Exploration Project
9/5/2000
![]() and
and ![]() are
estimated from the data, and we can interpret the first component as
signal, and the second component as noise, then the signal and noise
separation problem reduces to solving the least-squares system
are
estimated from the data, and we can interpret the first component as
signal, and the second component as noise, then the signal and noise
separation problem reduces to solving the least-squares system

![]() parameter in
equation (23) could clean up the signal estimate, but it
would also bring some of the signal into the subtracted noise. A
better strategy is to separate the events by using both the difference
in frequency and the difference in slope. For that purpose, I adopted
the following algorithm:
parameter in
equation (23) could clean up the signal estimate, but it
would also bring some of the signal into the subtracted noise. A
better strategy is to separate the events by using both the difference
in frequency and the difference in slope. For that purpose, I adopted
the following algorithm:

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)


![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)