Next: B-spline regularization
Up: Two-dimensional environmental data examples
Previous: Chernobyl rainfall in Switzerland
The next example is the SeaBeam dataset, a result of water bottom
measurements from a single day of acquisition. This dataset has been
used at the Stanford Exploration Project for benchmarking different
strategies of data interpolation
Clapp (2000b); Crawley (1995a,b); Fomel et al. (1997); Fomel (1996a, 2000a).
The left plot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the original data. The
right plot shows the result of (unpreconditioned) missing data
interpolation with the Laplacian filter. The result is
unsatisfactory, because the Laplacian filter does not absorb the
spatial frequency distribution of the input dataset. We judge the
quality of an interpolation scheme by its ability to hide the
footprints of the acquisition geometry in the final result.
shows the original data. The
right plot shows the result of (unpreconditioned) missing data
interpolation with the Laplacian filter. The result is
unsatisfactory, because the Laplacian filter does not absorb the
spatial frequency distribution of the input dataset. We judge the
quality of an interpolation scheme by its ability to hide the
footprints of the acquisition geometry in the final result.
seabdat
Figure 20 On the left, the
SeaBeam data: the depth of the ocean under ship tracks; on the
right, an interpolation with the Laplacian filter.





We can obtain a significantly better result (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
by replacing the Laplacian filter with a two-dimensional
prediction-error filter (PEF) estimated from the input data. The
result in the left plot of Figure
)
by replacing the Laplacian filter with a two-dimensional
prediction-error filter (PEF) estimated from the input data. The
result in the left plot of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) was obtained after
200 conjugate-gradient iterations. If we stop after 20 iterations, the
output (the right plot in Figure
was obtained after
200 conjugate-gradient iterations. If we stop after 20 iterations, the
output (the right plot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) shows only a small
deviation from the input data. Large areas of the image remain
unfilled. At each iteration, the interpolation process progresses only
to the length of the filter.
) shows only a small
deviation from the input data. Large areas of the image remain
unfilled. At each iteration, the interpolation process progresses only
to the length of the filter.
seabold
Figure 21 SeaBeam interpolation
with the prediction-error filter. The left plot was taken after 200
conjugate-gradient iterations; the right after 20 iterations.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





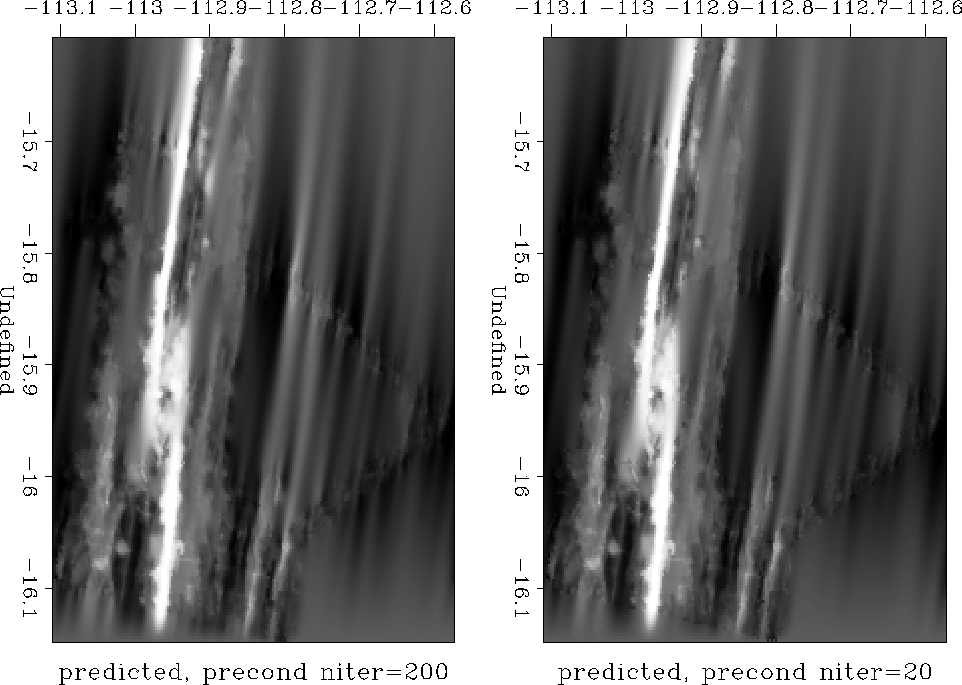
Inverting the PEF convolution with the help of the helix transform, we
can now apply the inverse filtering operator to precondition the
interpolation problem. As expected, the result after 200 iterations
(the left plot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is similar to the result
of the corresponding unpreconditioned interpolation. However, the
output after just 20 iterations (the right plot in Figure
) is similar to the result
of the corresponding unpreconditioned interpolation. However, the
output after just 20 iterations (the right plot in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is already fairly close to the solution.
)
is already fairly close to the solution.
seabnew
Figure 22 SeaBeam interpolation
with the inverse prediction-error filter. The left plot was taken after 200
conjugate-gradient iterations; the right, after 20 iterations.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: B-spline regularization
Up: Two-dimensional environmental data examples
Previous: Chernobyl rainfall in Switzerland
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the original data. The
right plot shows the result of (unpreconditioned) missing data
interpolation with the Laplacian filter. The result is
unsatisfactory, because the Laplacian filter does not absorb the
spatial frequency distribution of the input dataset. We judge the
quality of an interpolation scheme by its ability to hide the
footprints of the acquisition geometry in the final result.
shows the original data. The
right plot shows the result of (unpreconditioned) missing data
interpolation with the Laplacian filter. The result is
unsatisfactory, because the Laplacian filter does not absorb the
spatial frequency distribution of the input dataset. We judge the
quality of an interpolation scheme by its ability to hide the
footprints of the acquisition geometry in the final result.


![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)