|
cup
Figure 32 Reflector model for the constant-velocity test | 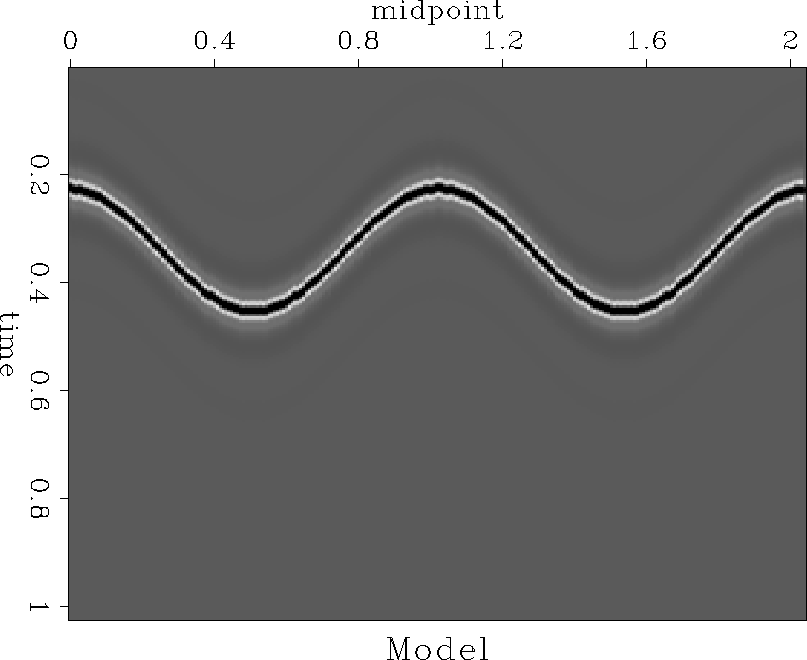 |
|
cup
Figure 32 Reflector model for the constant-velocity test |  |
A sinusoidal reflector shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) creates
complicated reflection data, shown in Figures
creates
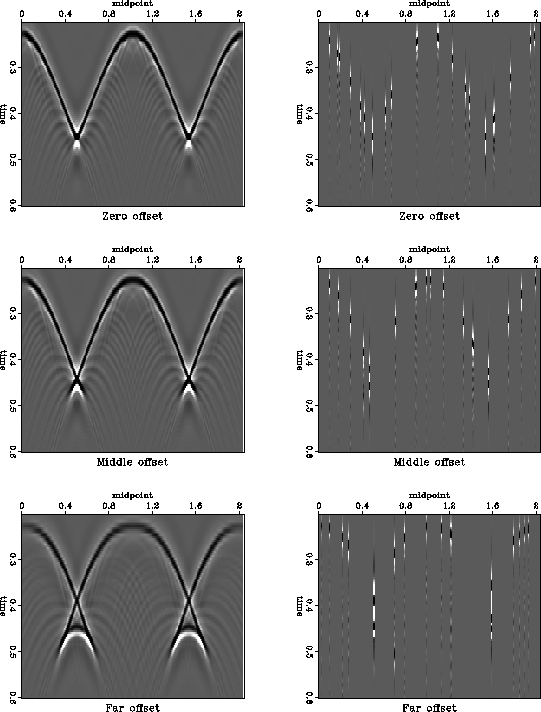
complicated reflection data, shown in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . To set up a test for regularization by offset
continuation, I removed 90% of randomly selected shot gathers from
the input data. The syncline parts of the reflector lead to
traveltime triplications at large offsets. A mixture of different dips
from the triplications would make it extremely difficult to
interpolate the data in individual common-offset gathers, such as
those shown in Figure
. To set up a test for regularization by offset
continuation, I removed 90% of randomly selected shot gathers from
the input data. The syncline parts of the reflector lead to
traveltime triplications at large offsets. A mixture of different dips
from the triplications would make it extremely difficult to
interpolate the data in individual common-offset gathers, such as
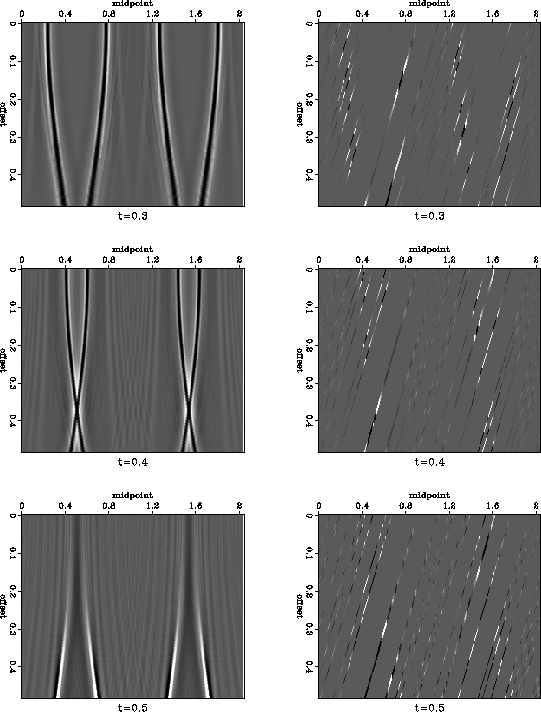
those shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The plots of time slices
after NMO (Figure
. The plots of time slices
after NMO (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) clearly show that the data are
also non-stationary in the offset direction. Therefore, a simple
offset interpolation scheme is also doomed.
) clearly show that the data are
also non-stationary in the offset direction. Therefore, a simple
offset interpolation scheme is also doomed.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
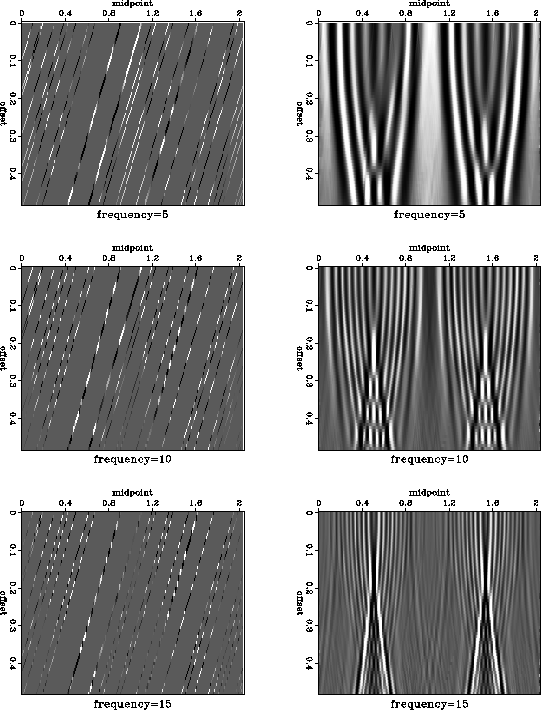
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the reconstruction process on individual
frequency slices. Despite the complex and non-stationary character of
the reflection events in the frequency domain, the offset continuation
equation is able to reconstruct them quite accurately from the
decimated data.
shows the reconstruction process on individual
frequency slices. Despite the complex and non-stationary character of
the reflection events in the frequency domain, the offset continuation
equation is able to reconstruct them quite accurately from the
decimated data.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of interpolation after the data
are transformed back to the time domain. The offset continuation
result (right plots in Figure
shows the result of interpolation after the data
are transformed back to the time domain. The offset continuation
result (right plots in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) reconstructs the ideal
data (left plots in Figure
) reconstructs the ideal
data (left plots in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) very accurately even in
the complex triplication zones, while the result of simple offset
interpolation (left plots in Figure
) very accurately even in
the complex triplication zones, while the result of simple offset
interpolation (left plots in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) fails as expected.
) fails as expected.
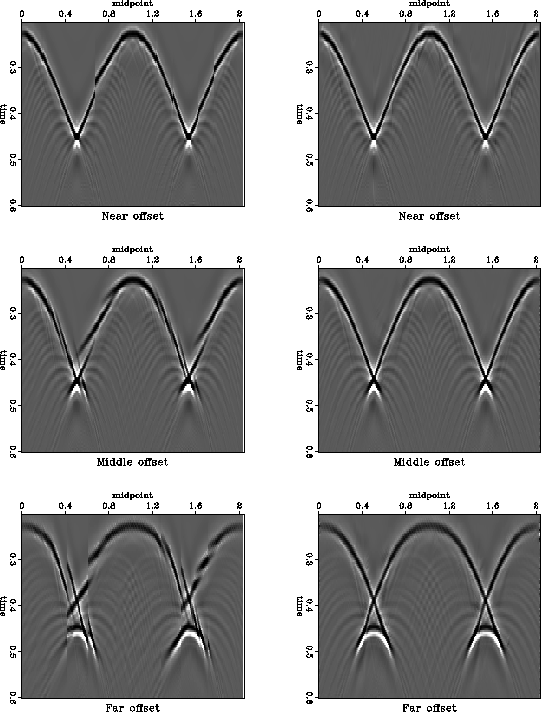 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Top, center, and bottom plots correspond
to different common-offset gathers.
. Top, center, and bottom plots correspond
to different common-offset gathers.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
The constant-velocity test results allow us to conclude that, when all the assumptions of the offset continuation theory are met, it provides a powerful method of data regularization.
Being encouraged by the synthetic results, I proceed to a three-dimensional real data test.