




Next: Filtering the coherent noise
Up: Guitton: Coherent noise attenuation
Previous: Introduction
To address the delicate problem of estimating
the noise covariance matrix Tarantola (1987), while building on
Claerbout and Fomel (1999), I have proposed to use a PEF for the
approximation Guitton (2000).
The PEF is estimated from a noise model or from the residual
of a previous inversion. In this paper, I show that both
methods filter the noise components as long as the PEF incorporates
enough spectral information for the noise. Because the noise covariance
matrix is supposed to filter out the inconsistent part of the
data (the coherent noise), I call this method the filtering
method. It is based on the following fitting goal:
| 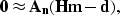 |
(1) |
where 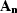 is a PEF estimated from the residual or from
a noise model,
is a PEF estimated from the residual or from
a noise model, 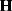 denotes a seismic operator,
denotes a seismic operator,  is the
model we seek, and
is the
model we seek, and 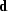 the seismic data. The corresponding least-squares
inverse, or the pseudo-inverse of
the seismic data. The corresponding least-squares
inverse, or the pseudo-inverse of  , is given by the equation
, is given by the equation
| 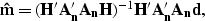 |
(2) |
where ( ) is the adjoint operator. The model space is computed
iteratively rather than by using the direct inversion described in
equation (2). I use two distinct strategies to compute the PEF
) is the adjoint operator. The model space is computed
iteratively rather than by using the direct inversion described in
equation (2). I use two distinct strategies to compute the PEF
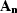 needed in equation (1).
With the first strategy, I derive a noise model from which a PEF is estimated
and kept unchanged, whereas with the second one, I compute the PEF from
the residual. I have slightly modified my inversion scheme described in
my earlier report Guitton (2000).
I propose the following algorithm when the PEF is estimated from the
residual:
needed in equation (1).
With the first strategy, I derive a noise model from which a PEF is estimated
and kept unchanged, whereas with the second one, I compute the PEF from
the residual. I have slightly modified my inversion scheme described in
my earlier report Guitton (2000).
I propose the following algorithm when the PEF is estimated from the
residual:
- 1.
- Solve the inverse problem for the fitting goal 0
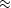 Hm - d.
Hm - d.
- 2.
- Estimate a PEF
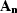 from the residual when only
coherent noise remains in the residual.
from the residual when only
coherent noise remains in the residual.
- 3.
- Restart the inverse problem (
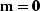 ) for the fitting
goal in equation (1).
) for the fitting
goal in equation (1).
- 4.
- Iterate with the new PEF.
- 5.
- Reestimate the PEF
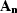 from the residual Hm - d.
from the residual Hm - d.
- 6.
- Go to step (4).
- 7.
- Stop when the residual has a white spectrum.
The novelty of this algorithm is that the first PEF is
not estimated from the data but rather from the residual of
a previous inverse problem where no PEF is used in the fitting goal.
This has the advantage of isolating the coherent noise more accurately,
thus furnishing a satisfying noise model for the PEF estimation.
This algorithm can be seen as a two-stage process in which the first
stage helps to estimate a first PEF for our
inversion and the second stage reestimates the PEF iteratively.
Determining when to stop the inversion to compute the first PEF is
critical: too many iterations and the coherent noise is fitted,
too few and some signal remains in the residual.
The filtering method is viable if the operator 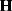 does not
model the coherent noise properly. In other words, the signal
is expected to be orthogonal to the coherent noise for proper
attenuation.
does not
model the coherent noise properly. In other words, the signal
is expected to be orthogonal to the coherent noise for proper
attenuation.
The sections that follow describe the application of this method with
synthetic and real data. For each case,
I estimate the PEF from a noise model or from the residual of
a previous inversion. My results demonstrate that both methods lead to a proper
attenuation of the noise components.





Next: Filtering the coherent noise
Up: Guitton: Coherent noise attenuation
Previous: Introduction
Stanford Exploration Project
4/29/2001