Results with the frequency domain approach

I implemented this method with synthetic and real data. The synthetic case perfectly attenuates the aliasing artifacts. The real data case is not as convincing however, because we have a dense information in the data space to interpret with few parabolas in the model space.

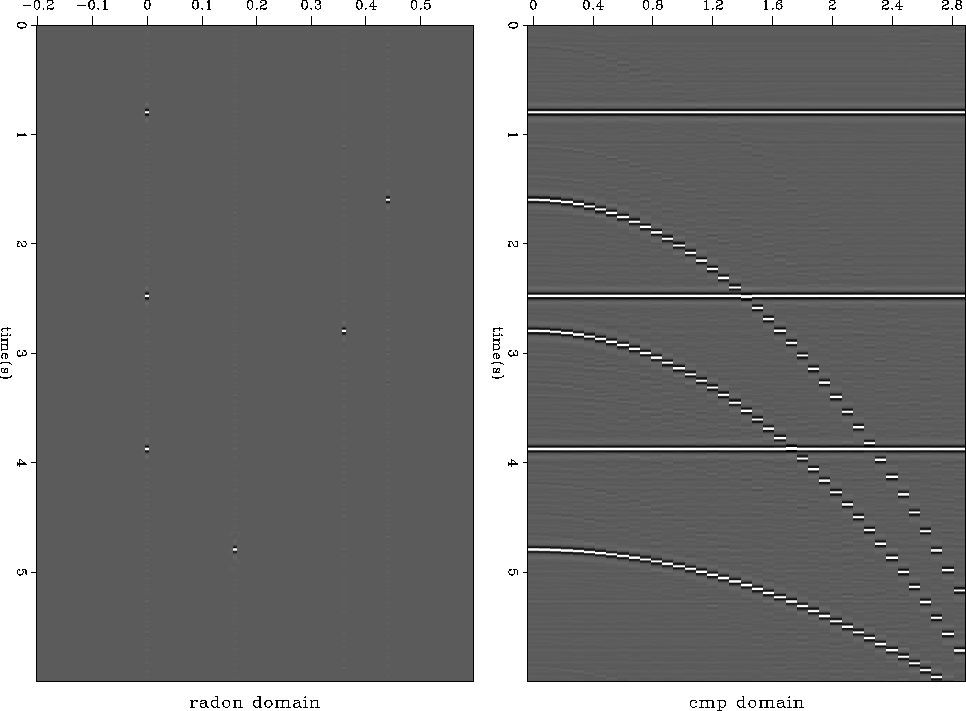
The result with synthetic data is striking (Figure 8): all the artifacts have disappeared, leaving a clean model space. The data are almost entirely recovered. Figure 9 displays the diagonal elements of the matrix 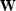${\bf W}$ at each frequency. We can see that from the lowest to the highest frequencies, the diagonal elements focus at four different locations corresponding to the four parabolic curvatures present in the input data. The cut-off at 70 Hz which corresponds to the highest frequency component present in the data, is used to calculate the model space.

 

spikeal
Figure 8 Left: Model space using the steering matrices. Right: Data reconstructed from the left panel. The aliasing artifacts are gone, and the focusing in the model space is perfect.

 

weight Figure 9 Diagonal elements of the weighting matrix ${\bf W}$ at each frequency. The four stripes correspond to the location of the four curvatures in the radon domain. The cutoff at 70 Hz corresponds to the highest frequency present in the data.

With real data, however, the results suggest strategies to better focus the radon domain. Figure 10 shows the inversion of one CMP gather in the parabolic radon domain when no attempt were made to focus the model space components, that is, no weight in equation (23). The residual is displayed in the right panel of Figure 12. Although the inversion produces a satisfactory fitting of the input data, some aliasing artifacts appear in the radon domain. Figure 11 displays the result of the inversion using the steering-weighting matrices. It shows that fewer artifacts appear in the radon domain. A comparison of the residual with and without weight , shown in Figure 12, demonstrates that the data fitting is satisfactory for both cases. It turns out that the crucial parameter is 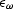$\epsilon_{\omega}$. I don't have any guideline for choosing it but trial and error. The efficiency of the steering-weighting matrices method is based on the number of parabolic events present in the data. The best results are achieved when few events have to be focused in a large radon domain. However, since for real data cases this requirement may be difficult to meet, I anticipate no or few improvements if we use this method. One solution may be simply to apply it to different patches as suggested by Herrmann et al. (2000).

 

nmo2
Figure 10 Left: A radon domain obtained using inversion without steering matrices. Right: The reconstructed data.

 

nmo1
Figure 11 Left: A radon domain obtained using inversion with steering matrices. Right: The reconstructed data.

 

comp2
Figure 12 Left: Residual of the inversion in Figure 10 using the steering matrices. Middle: Input data. Right: Residual of the inversion in Figure 11 without the steering matrices.