Redefining R

The principle of causality: no response before a stimulus, is not considered in the R definition [equation (2)]. The omission of causality translates into improper behavior of the high frequencies. In order to include causality into the definition of R, let $s=-i\hat{\omega}$ be the causal, positive, discrete representation of the differentiation operator,

$$s=-i\hat{\omega} = \frac{2}{\Delta t} \frac{1-\rho Z}{1+ \rho Z},$$ (3)

which is simplified by writting $s=-i\omega + \epsilon$.

Claerbout (1985) proposes the use of the following Muir recursion starting from R₀=s:

 

$$R_{n+1} = s + \frac{X^{2}}{s + R_{n}}.$$ (4)

This recursion produces a continuous fraction. Studying the limit for $n \rightarrow \infty$we obtain:

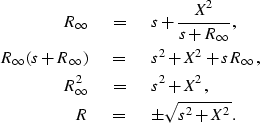$$\begin{eqnarray} R_{\infty} \ \ & = & \ \ s + \frac{X^{2}}{s + R_{\infty}}, \non... ...2} + X^{2}, \nonumber \\ R \ \ & = & \ \ \pm \sqrt{s^{2} + X^{2}}.\end{eqnarray}$$ (5)

If we let X² = v² k_x² in equation (5) then R is $\pm ik_{z}v$. The retarded time expression of $e^{-R\frac{z}{v}}$ [equation (6)] will downward continue, in time, the data for phase-shift migration.

 

$$e^{-R\frac{z}{v}} = e^{-(R - s) \frac{z}{v}} e^{-s \frac{z}{v}}.$$ (6)

The following change of variables:

$$R^{\prime} = R - s$$ (7)

transforms the Muir recursion (4) into:

 

$$R^{\prime}_{n+1} = \frac{v^{2} k_{x}^{2}}{2s + R^{\prime}_{n}}.$$ (8)

Again, taking the limit for $n \rightarrow \infty$ in this recursion we will obtain

$$\begin{eqnarray} R^{\prime}_{\infty} \cdot (2s + R^{\prime}_{n}) \ \ & = & \ \ v... ...ty}}^{2} + 2sR^{\prime}_{\infty} - v^{2} k_{x}^{2} \ \ & = & \ \ 0\end{eqnarray}$$ (9)

This quadratic expression yields to two square roots for $R^{\prime}$,

$$R^{\prime} = -s \pm \sqrt{s^{2} + v^{2} k_{x}^{2}}.$$ (10)

We need to select the one that is able to handle the evanescent region, i.e, the square root that goes to zero at k_x = 0, which corresponds to the positive square root.

 

$$R^{\prime} = -s + \sqrt{s^{2} + v^{2} k_{x}^{2}},$$ (11)

multiplying numerator and denominator by $s+\sqrt{s^{2} + v^{2} k_{x}^{2}}$, equation (11) transforms into:

 

$$R^{\prime} = \frac{v^2 k_x^2}{\sqrt{s^{2} + v^{2} k_{x}^{2}} + s}.$$ (12)

I already showed that the real part of $\sqrt{s^{2} + v^{2} k_{x}^{2}}$ is positive (Figure 1); therefore, $R^{\prime}$, as defined in equation (12), also has a positive real part.

Finally, we downward continue the data in the Fourier domain by multiplying by:

 

$$e^{-R^{\prime} \frac{z}{v}} e^{-i\omega \frac{z}{v}}$$ (13)

Expression (13) incorporates the causality and viscosity concepts in phase shift migration, controls the evanescent energy and will not allow discontinuity between evanescent and non-evanescent regions.