Angle domain common image gathers

Both de Bruin et al. (1991) and Prucha et al. (1999) obtain P-wave angle-domain common-image gathers by slant-stacking the wavefields during migration, before invoking the imaging condition. Their methodologies suit shot-profile and shot-geophone algorithms, respectively. However, we follow an alternative approach advocated by Sava and Fomel (2000).

Fomel (1996) presented the following partial differential equation describing an image surface in depth-midpoint-offset space:

$$\tan \theta = - \left. \frac{\partial z}{\partial h}\right\vert _{t,x},$$ (1)

where $\theta$ is the P-wave opening or incidence angle.

For converted waves, $\theta$ has a no simple physical interpretation. In this case, $\theta$ is a complex function of the P-incidence angle, the S-reflection angle, and the structural dip, $\alpha$ (Figure 3). Figure 3 shows the geometrical relationship between the P-incidence angle, the S-reflection angle, and the structural dip with the opening angle for the converted waves case. Following Fomel's 1996 derivation we will derive the PS relationship for angle domain common image gathers. In order to relate the first-order traveltime derivatives of the PS-wave with the P-incidence angle and the S-reflection angle, we use the well-known equations for apparent slowness

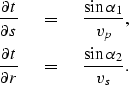$$\begin{eqnarray} \frac{\partial t}{\partial s} \ \ & = & \ \ \frac{\sin \alpha_1... ...c{\partial t}{\partial r} \ \ & = & \ \ \frac{\sin \alpha_2}{v_s}.\end{eqnarray}$$ (2) (3)

 

sergey Figure 3 Reflection rays for a PS-data in a constant velocity medium (Adapted from Fomel 1996).

Considering the traveltime derivative with respect to the depth of the observation surface (z), the contributions of the two branches of the reflected ray add together to form

 

$$- \frac{\partial t}{\partial z} = \frac{\cos \alpha_1}{v_p} + \frac{\cos \alpha_2}{v_s}.$$ (4)

Introducing midpoint $x = \frac{s+r}{2}$ and half-offset $h = \frac{r-s}{2}$ coordinates, and relating $\alpha_1$ and $\alpha_2$ with the P-incidence angle ($\beta_p$), the S-reflection angle ($\beta_s$), and the structural dip ($\alpha$)

$$\begin{eqnarray} \alpha_1 \ \ & = & \ \ \alpha - \beta_{p}, \nonumber \\ \alpha_2 \ \ & = & \ \ \alpha + \beta_{s}; \nonumber\end{eqnarray}$$

and using the chain rule:

$$\begin{eqnarray} \frac{\partial t}{\partial x} \ \ & = & \ \ \frac{\partial t}{\... ...{\partial t}{\partial r}-\frac{\partial t}{\partial s}. \nonumber \end{eqnarray}$$

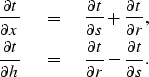We can transform relations (2), (3), and (4) to:

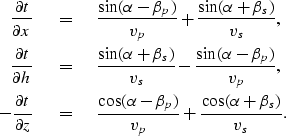$$\begin{eqnarray} \frac{\partial t}{\partial x} \ \ & = & \ \ \frac{\sin(\alpha-\... ...\frac{\cos(\alpha-\beta_p)}{v_p}+\frac{\cos(\alpha+\beta_s)}{v_s}.\end{eqnarray}$$ (5) (6) (7)

Dividing (6) by (7) and using elementary trigonometric equalities, we obtain:

 

$$- \frac{\partial z}{\partial h} = \frac{v_p \sin \alpha \cos... ...lpha \cos \beta_p + v_s \sin \alpha \sin \beta_p} = \tan \theta$$ (8)

For v_p = v_s, the P-incidence angle will be the same as the S-reflection angle; hence, $\theta$ in equation (8) corresponds to the ray incidence angle. However, for converted waves ($v_p \neq v_s$) no such simple physical interpretation exists, and $\theta$ relates the P-incidence angle, the S-reflection angle, and the structural dip.

For the determination of the polarity flip in the angle domain we define $\theta_o$ as the polarity flip angle, for which the P-incidence angle equals the S-reflection angle and they are both equal to zero ($\beta_p = \beta_s = 0$), i.e normal incidence. Thus $\theta_o$ corresponds to the point of polarity flip in angle domain. Equation (8) reduces to:

 

$$\tan \theta_o =\tan \alpha \frac{v_p - v_s}{v_p + v_s}=\tan \alpha \frac{\gamma-1}{\gamma+1}.$$ (9)

It is important to emphasize that for constant $\gamma$ the polarity flip will not necessarily occur at $\theta = 0$ because of the reflector dip effect.