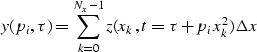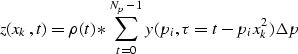Next: Geological Target
Up: Alvarez: Multiple suppression
Previous: Introduction
Primary reflections in a common midpoint gather exhibit a hyperbolic
moveout as a function of offset (gray lines on the left of
Figure 3). The governing equation of the hyperbolic moveout
is:
| 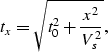 |
(1) |
where tx corresponds to the arrival time of the reflection at
offset x,
t0 corresponds to the arrival time at zero offset and Vs is the
NMO-stacking
velocity. This velocity is the one that best fits the moveout of the hyperbola
and is determined by trial and error from among a series of probable
velocities. If correctly chosen, this velocity allows the moveout
corrected primary reflections to become horizontal
(solid black horizontal lines in left of Figure 3).
Clearly the selection of the stacking velocities must
be done to correct for the moveout of the primary reflections and not for the
multiples. At a given zero-offset arrival time the velocity of a primary
reflection is greater than that of a multiple, which according to
Equation (1) implies a smaller moveout. This difference in moveout
makes it possible to flatten the primary reflections while leaving the
multiples under-corrected with a moveout approximately parabolic
Hampson (1986). The Parabolic Radon Transform exploits this difference by
summing trace amplitudes along parabolas of different zero-offset time and
curvature. Hence, the transform can be
considered a mathematical operator that maps parabolas in the t-x domain
to small regions of the parabolic moveout (p) and zero-offset time
( ) domain.
) domain.
mul_esq2
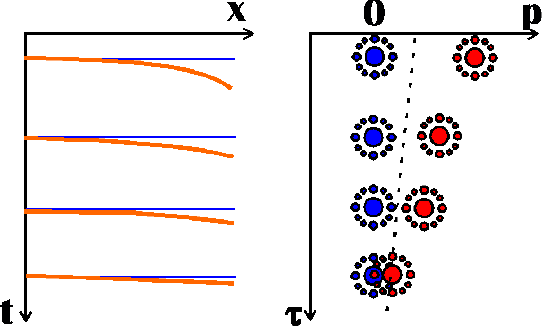
Figure 3 Schematic representation of multiple
suppression by filtering in the parabolic Radon transform domain. Left:
t-x domain, right:  -p domain.
-p domain.

This is schematically shown in Figure 3 which shows
that the horizontal events in t-x domain map to a vertical strip in the
 -p domain at p=0. The multiple reflections, on the other hand, are
mapped in the
-p domain at p=0. The multiple reflections, on the other hand, are
mapped in the  -p domain to a region away from the p=0 vertical
line. This separation allows for the suppression of the multiple energy by
zeroing out the
-p domain to a region away from the p=0 vertical
line. This separation allows for the suppression of the multiple energy by
zeroing out the  -p region to the right of the dashed line
in Figure 3. The inverse
-p region to the right of the dashed line
in Figure 3. The inverse  -p transform would then
return the primaries to the t-x domain.
-p transform would then
return the primaries to the t-x domain.
In practice the process is applied a little
differently: it is the energy of the primaries that is suppressed
(energy to the left of the dashed line in Figure 3)
and inversely transformed to the t-x domain. The primaries
are computed by subtracting the multiples from the original data in this
domain. This method was first introduced with the name ``inverse velocity
stacking'' Hampson (1986).
The mathematical equivalent of the qualitative description given
before for the Parabolic Radon Transform is a set of two equations:
| 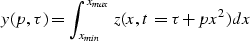 |
(2) |
| 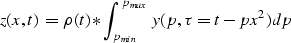 |
(3) |
The first equation corresponds to the forward transform (from
t-x to
 -p) and the second one to the inverse transform (from
-p) and the second one to the inverse transform (from  -p to
t-x). z and y represent the trace amplitudes in t-x and
-p to
t-x). z and y represent the trace amplitudes in t-x and
 -p domain respectively. xmin and xmax correspond to the
minimum and
maximum CMP offset, pmin and pmax to the minimum and maximum parabola
curvature used in the transform, and, as usual, the symbol
-p domain respectively. xmin and xmax correspond to the
minimum and
maximum CMP offset, pmin and pmax to the minimum and maximum parabola
curvature used in the transform, and, as usual, the symbol  denotes
convolution. It is
interesting to note that except for the difference in sign and the presence
of the
denotes
convolution. It is
interesting to note that except for the difference in sign and the presence
of the 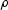 term, the equations for both transforms are basically the same. The term
term, the equations for both transforms are basically the same. The term
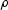 represents a filter that corrects the high frequency loss incurred in
the forward transform Claerbout (1995). In the case of continuous
functions
these transforms are exact inverses of one another. In seismic data processing
we deal with sampled information, however, which means that we need to use the
discrete equivalents of equations (2) and ( 3):
represents a filter that corrects the high frequency loss incurred in
the forward transform Claerbout (1995). In the case of continuous
functions
these transforms are exact inverses of one another. In seismic data processing
we deal with sampled information, however, which means that we need to use the
discrete equivalents of equations (2) and ( 3):
| 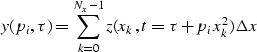 |
(4) |
| 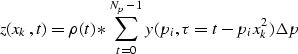 |
(5) |
where Nx and Np are the number of traces and parabolas
respectively.
The need to work with discrete equations may give raise to aliasing
problems
Yilmaz (1987) as well as to some stability problems related to the selection
of the number of parabolas used in the transform. In commercial
software packages the transform is normally implemented in the f-x domain
because of issues related to the amplitude of the inverse transform
which is computed via a numerical optimization process. The discussion of these
details, which are very important for the successful application of the
method, are out of the scope of this paper. See for example Anderson (1993)
and Alvarez (1995).





Next: Geological Target
Up: Alvarez: Multiple suppression
Previous: Introduction
Stanford Exploration Project
4/29/2001
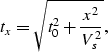
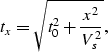
![]() ) domain.
) domain.
![]() -p domain at p=0. The multiple reflections, on the other hand, are
mapped in the
-p domain at p=0. The multiple reflections, on the other hand, are
mapped in the ![]() -p domain to a region away from the p=0 vertical
line. This separation allows for the suppression of the multiple energy by
zeroing out the
-p domain to a region away from the p=0 vertical
line. This separation allows for the suppression of the multiple energy by
zeroing out the ![]() -p region to the right of the dashed line
in Figure 3. The inverse
-p region to the right of the dashed line
in Figure 3. The inverse ![]() -p transform would then
return the primaries to the t-x domain.
-p transform would then
return the primaries to the t-x domain.