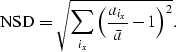Next: Computational cost
Up: Model-space weighting functions
Previous: Stabilizing the denominator
The Amoco 2.5-D synthetic dataset Etgen and Regone (1998)
provides an excellent test for the weighting functions discussed
above.
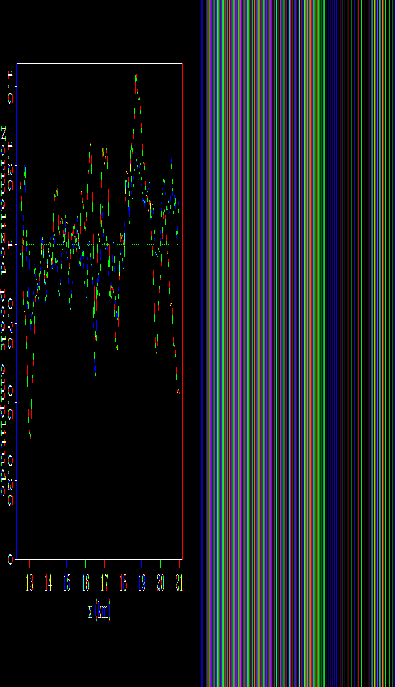
The velocity model (Figure 1) contains
significant structural complexity in the upper 3.8 km, and a flat
reflector of uniform amplitude at about 3.9 km depth.
Since the entire velocity model (``Canadian foothills overthrusting
onto the North Sea'') is somewhat pathological, I restricted my
experiments to the North Sea section of the dataset (x>10 km).
The data were generated by 3-D acoustic finite-difference modeling of
the 2.5-D velocity model.
However, making the test more difficult is the fact that the 2-D
linear one-way recursive extrapolators Ristow and Ruhl (1994) that I use for
modeling and migration do not accurately predict the 3-D geometric
spreading and multiple reflections that are present in this dataset.
amocovel
Figure 1 Velocity (in km/s) model used to
generate the synthetic Amoco 2.5-D dataset.





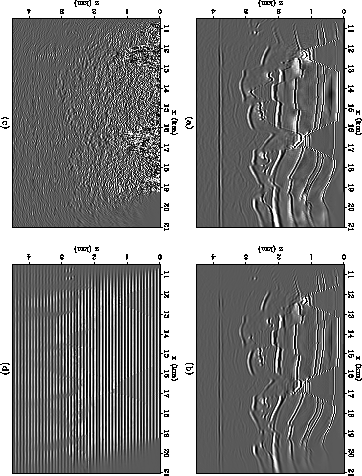
Figure 2 compares the migrated image ( )with the results of remodeling and remigrating the three reference
images described above. The imprint of the recording geometry is
clearly visible on the three remigrations in
Figures 2 (b-d).
)with the results of remodeling and remigrating the three reference
images described above. The imprint of the recording geometry is
clearly visible on the three remigrations in
Figures 2 (b-d).
Figure 3 compares the illumination calculated from
the three reference images with the raw shot illumination.
Noticably, the shot-only weighting function [panel (a)] does not take
into account the off-end (as opposed to split-spread) receiver geometry.
Panel (b), the weighting function derived from
model  , appears slightly noisy. However, in well-imaged
areas (e.g. along the target reflector), the weighting function is
well-behaved.
Panel (c) shows the weighting function derived from the random
reference image (
, appears slightly noisy. However, in well-imaged
areas (e.g. along the target reflector), the weighting function is
well-behaved.
Panel (c) shows the weighting function derived from the random
reference image ( ). Despite the smoothing, this weighting
function clearly bears the stamp of the random number field. A feature
of white noise is that no amount of smoothing will be able to
remove the effect of the random numbers completely.
The final panel (d) shows the flat-event illumination weighting
function, derived from
). Despite the smoothing, this weighting
function clearly bears the stamp of the random number field. A feature
of white noise is that no amount of smoothing will be able to
remove the effect of the random numbers completely.
The final panel (d) shows the flat-event illumination weighting
function, derived from 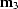 . This is noise-free and very
well-behaved since it depends only on the velocity model and recording
geometry, not the data.
. This is noise-free and very
well-behaved since it depends only on the velocity model and recording
geometry, not the data.
amocomigs
Figure 2 Comparison of calibration images:
(a) original migration, (b) original migration after modeling and
migration, (c) random image after modeling and migration, and (d) flat
event image after modeling and migration.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)




 amocowghts
amocowghts
Figure 3 Comparison of
weighting functions: (a) original migration, (b) original migration
after modeling and migration, (c) random image after modeling and
migration, and (d) flat event image after modeling and migration.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





For a quantitative comparison, I picked the maximum amplitude of the
3.9 s reflection event on the calibrated images.
The normalized standard deviation (NSD) of these
amplitudes is shown in Table 1, where
| 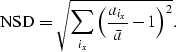 |
(7) |
Table 1, therefore, provides a measure of how well
the various weighting function compensate for illumination
difficulties.
The amplitudes of the raw migration, and the migration after
flat-event normalization are shown in Figure 4.
This illustrates the numerical results from Table 1:
for this model the normalization procedure improves amplitude
reliability by almost a factor of two.
Table 1:
Comparison of the reflector strength for different choices of
illumination-based weighting function.
| 2||c|Weighting function: |
NSD: |
|
| 2||c|No weighting function |
0.229 |
|
| 2||c|Shot illumination |
0.251 |
|
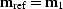 |
(migrated image) |
0.148 |
|---|
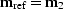 |
(random image) |
0.195 |
|---|
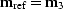 |
(flat events) |
0.140 |
|---|
eventamp
Figure 4 Normalized peak amplitude of 3.9 km
reflector after migration (solid line), and then normalization by
flat-event illumination (dashed line) derived with
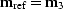 . The ideal result would be a constant
amplitude of 1. . The ideal result would be a constant
amplitude of 1.
|
|  |










Next: Computational cost
Up: Model-space weighting functions
Previous: Stabilizing the denominator
Stanford Exploration Project
4/29/2001


![]() )with the results of remodeling and remigrating the three reference
images described above. The imprint of the recording geometry is
clearly visible on the three remigrations in
Figures 2 (b-d).
)with the results of remodeling and remigrating the three reference
images described above. The imprint of the recording geometry is
clearly visible on the three remigrations in
Figures 2 (b-d).
![]() , appears slightly noisy. However, in well-imaged
areas (e.g. along the target reflector), the weighting function is
well-behaved.
Panel (c) shows the weighting function derived from the random
reference image (
, appears slightly noisy. However, in well-imaged
areas (e.g. along the target reflector), the weighting function is
well-behaved.
Panel (c) shows the weighting function derived from the random
reference image (![]() ). Despite the smoothing, this weighting
function clearly bears the stamp of the random number field. A feature
of white noise is that no amount of smoothing will be able to
remove the effect of the random numbers completely.
The final panel (d) shows the flat-event illumination weighting
function, derived from
). Despite the smoothing, this weighting
function clearly bears the stamp of the random number field. A feature
of white noise is that no amount of smoothing will be able to
remove the effect of the random numbers completely.
The final panel (d) shows the flat-event illumination weighting
function, derived from ![]() . This is noise-free and very
well-behaved since it depends only on the velocity model and recording
geometry, not the data.
. This is noise-free and very
well-behaved since it depends only on the velocity model and recording
geometry, not the data.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)