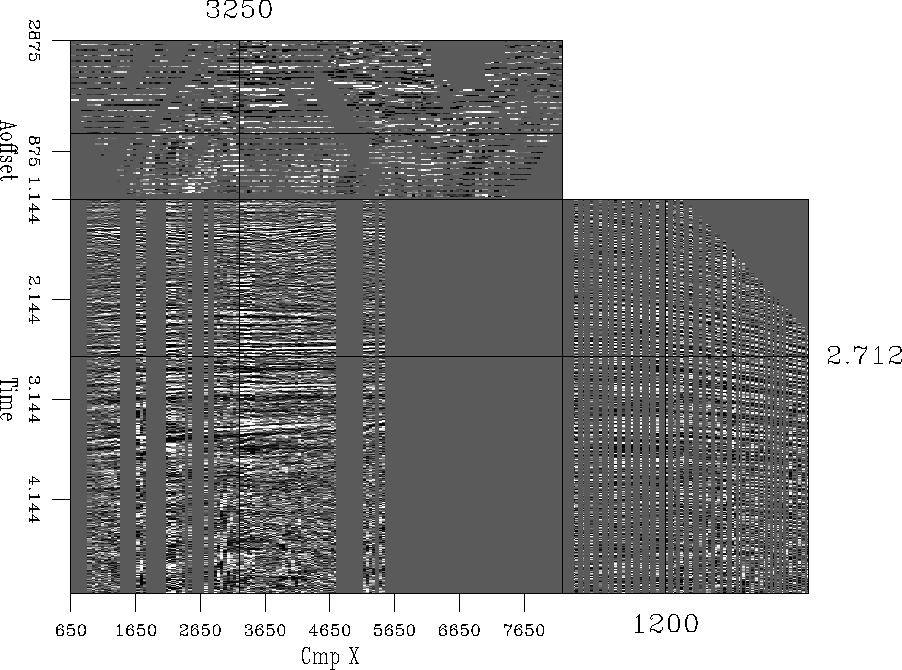
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the PP data
for one crossline of the data set in study. Observe the holes
in the data due to irregularities in the geometry acquisition.
presents the PP data
for one crossline of the data set in study. Observe the holes
in the data due to irregularities in the geometry acquisition.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the PP data
for one crossline of the data set in study. Observe the holes
in the data due to irregularities in the geometry acquisition.
presents the PP data
for one crossline of the data set in study. Observe the holes
in the data due to irregularities in the geometry acquisition.
 |
Biondi and Vlad 2001 examined the differences among regularizing the data with normalization, regularization with the leaky integration operator and regularization with the AMO operator. They conclude that the precondition of the regularized least-squares problem with the AMO operator yields more continuous results.
On this part of the problem, we only present the
final interpolation results using normalization and
AMO regularization. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents the fold maps
calculated using both normalization (top) and AMO regularization
(bottom). Note that even though the fold maps are similar,
as expected, the fold distribution is smoother using AMO regularization.
Also note that with AMO regularization, the fold reduces to the half.
This fact affects the final solution of the least-squares problem.
presents the fold maps
calculated using both normalization (top) and AMO regularization
(bottom). Note that even though the fold maps are similar,
as expected, the fold distribution is smoother using AMO regularization.
Also note that with AMO regularization, the fold reduces to the half.
This fact affects the final solution of the least-squares problem.
|
fold
Figure 3 Fold, using normalization (top) and AMO regularization (bottom) |  |
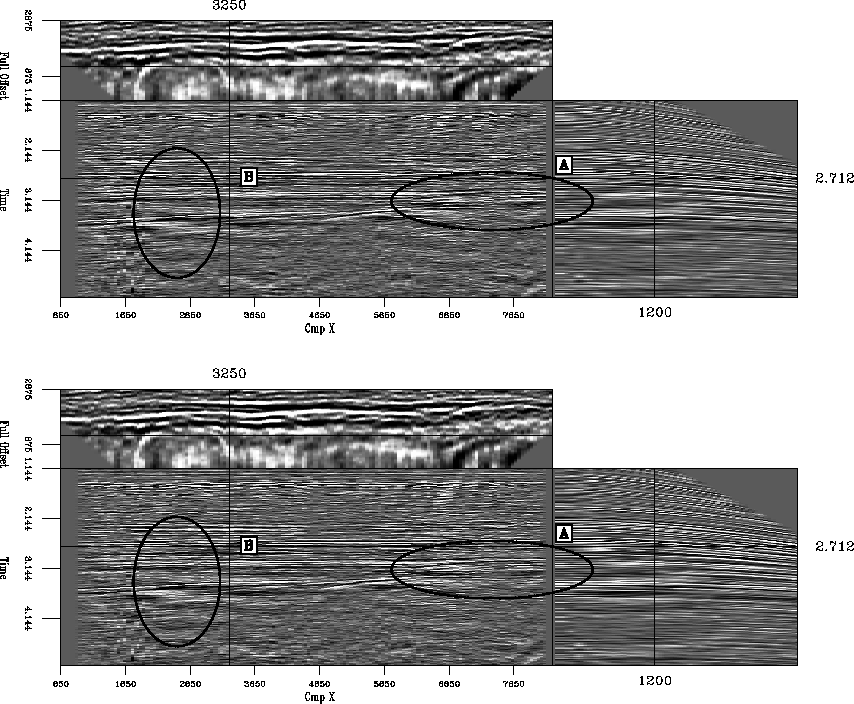
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the result of geometry regularization using
normalization (top) and AMO regularization (bottom). Differences
lie in the amplitudes and the borders.
compares the result of geometry regularization using
normalization (top) and AMO regularization (bottom). Differences
lie in the amplitudes and the borders.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)