




Next: CONCLUSIONS
Up: 1-D Super Dix
Previous: 1-D Super Dix
Now we have almost all of the pieces to create multiple
realistic interval velocity models from
our 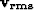 measurements.
The left panel of Figure
measurements.
The left panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the residual
after estimating the model using (15). We can see
that there is a low frequency component to the residual.
We can estimate a PEF from this residual and
resolve (15) using
shows the residual
after estimating the model using (15). We can see
that there is a low frequency component to the residual.
We can estimate a PEF from this residual and
resolve (15) using
| 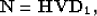 |
(16) |
where  is convolution with our PEF calculated
from the residual.
The resulting residual (right panel of Figure
is convolution with our PEF calculated
from the residual.
The resulting residual (right panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is now
white.
) is now
white.
dix3
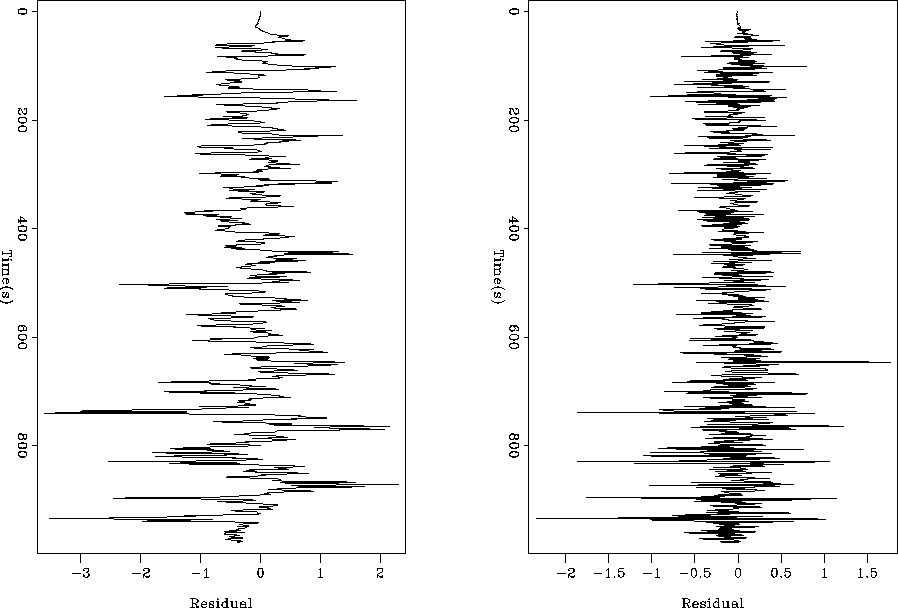
Figure 14 The left panel
is the residual without using a whitening filter. The
right panel is the residual using a whitening filter.
Note how the residual is showing only minimal structure.
|
|  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





We can now use our multiple realization machinery
to produce multiple interval velocity models that
have approximately the correct covariance.
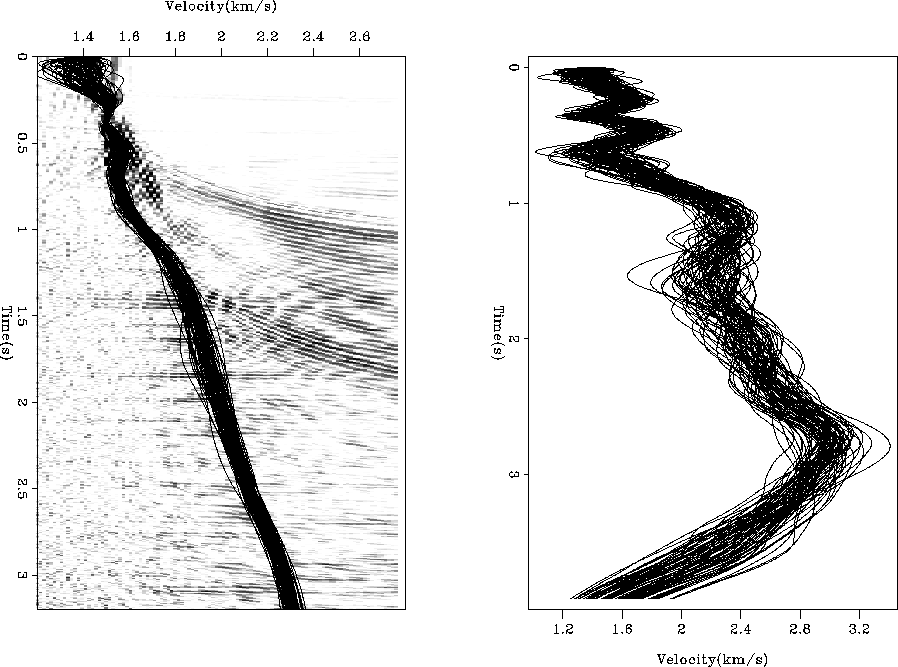
The right panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows 80 interval velocity
realizations. The left panel shows those realizations
converted back to
shows 80 interval velocity
realizations. The left panel shows those realizations
converted back to 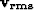 . Note how the
. Note how the 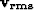 functions
stay within variance bounds. In addition, as we expected,
we see larger
variance where our bounds are wider.
If we look at the mean
and variance of our interval and rms (Figure
functions
stay within variance bounds. In addition, as we expected,
we see larger
variance where our bounds are wider.
If we look at the mean
and variance of our interval and rms (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
estimates we get another interesting result.
Areas of large variance are not always correlated.
)
estimates we get another interesting result.
Areas of large variance are not always correlated.
dix4
Figure 15 The right panel shows 80 interval velocity realizations.
The left panel show those interval velocities
converted back to 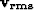 overlaying the stack power for
the CMP gather.
overlaying the stack power for
the CMP gather.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





dix5
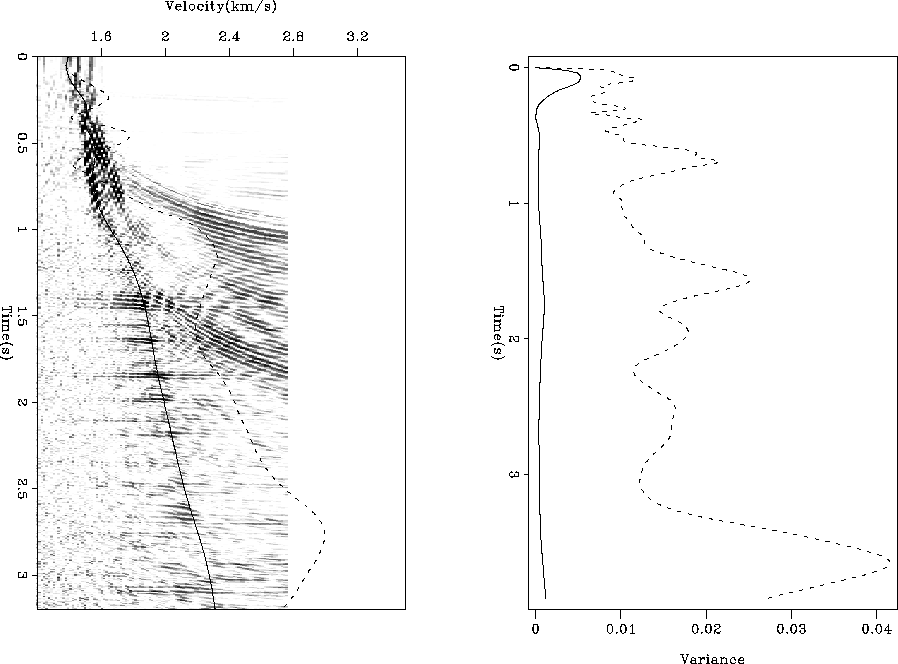
Figure 16 The left panel shows the mean of the
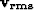 (solid line) and (solid line) and
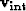 (dashed line) of 80 realizations overlaying the stack power.
The right panel shows the variance of (dashed line) of 80 realizations overlaying the stack power.
The right panel shows the variance of 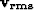 and and 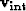 for
the 80 realizations. for
the 80 realizations.
|
|  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: CONCLUSIONS
Up: 1-D Super Dix
Previous: 1-D Super Dix
Stanford Exploration Project
7/8/2003
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the residual
after estimating the model using (15). We can see
that there is a low frequency component to the residual.
We can estimate a PEF from this residual and
resolve (15) using
shows the residual
after estimating the model using (15). We can see
that there is a low frequency component to the residual.
We can estimate a PEF from this residual and
resolve (15) using
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is now
white.
) is now
white.

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows 80 interval velocity
realizations. The left panel shows those realizations
converted back to
shows 80 interval velocity
realizations. The left panel shows those realizations
converted back to ![]() . Note how the
. Note how the ![]() functions
stay within variance bounds. In addition, as we expected,
we see larger
variance where our bounds are wider.
If we look at the mean
and variance of our interval and rms (Figure
functions
stay within variance bounds. In addition, as we expected,
we see larger
variance where our bounds are wider.
If we look at the mean
and variance of our interval and rms (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
estimates we get another interesting result.
Areas of large variance are not always correlated.
)
estimates we get another interesting result.
Areas of large variance are not always correlated.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)