PROBLEMS

Getting fitting goals (9) to work correctly requires a good handle on several elements that are not necessarily easy or even possible to achieve. To demonstrate these problems, I am going to set up a simple deblurring inversion problem. The left panel of Figure  shows the model $\bf m$ that we are going to attempt to invert for. The right panel of Figure  shows the data $\bf d$, the model blurred by a simple known filter. If we add random noise to the problem (left panel of Figure ), we can quickly get an unreasonable model estimate (right panel of Figure ). If we add an isotropic regularizer, our estimate improves substantially (Figure ). We will speed up the conversion of our problem by preconditioning the problem $\bf A^{-1}$ with a symmetric operator and start with

$$\begin{eqnarray} \bf 0&\approx&\bf r_{d} = \bf N_{noise}( \bf d- \bf L\bf A^{-1}\bf p) \nonumber \\ \bf 0&\approx&\bf r_{m} = \epsilon \bf p\end{eqnarray}$$ (10)

as our fitting goals.

 

unblur1
Figure 3 The left panel is the model that we are going to attempt to invert for. The right panel is the data, a blurred version of the model.

 

rand
Figure 4 The left panel is the data with Gaussian random noise added. The right panel is the resulting model estimate.

 

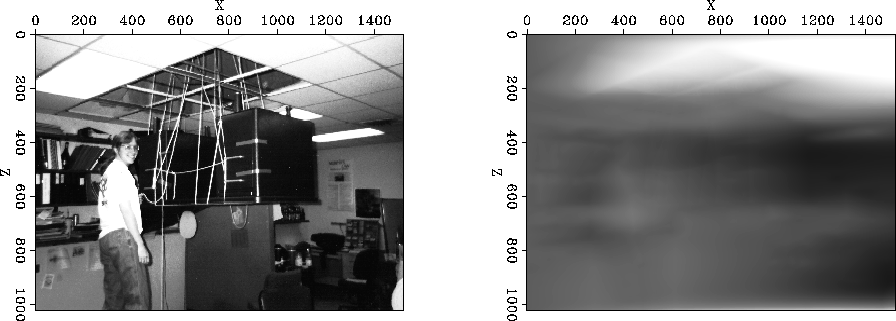
rand2 Figure 5 The model estimated from the data shown in the left panel of Figure  using an isotropic regularization operator.