Euler-Lagrange solution for flattening

The Euler-Lagrange equation can be used to find the absolute time (t(x,y)) that minimizes (Fomel, 2002, personal communication)  

$$J(t) = \int \int \left[ \left( p_x(t,x,y)-\frac{\partial t}{... ...(t,x,y)-\frac{\partial t}{\partial y}\right)^2 \right] \,dx\,dy$$ (16)

where p_x is the dip in the x direction and p_y is the dip in the y direction.

This can be simplified for the 2-D case to find the absolute time (t(x)) that minimizes  

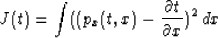$$J(t) = \int((p_x(t,x)-\frac{\partial t}{\partial x})^2 \,dx$$ (17)

The Euler-Lagrange equation Farlow (1993) is used to find the function (t(x)) that minimizes the equation of this form  

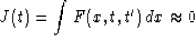$$J(t) = \int F(x,t,t') \,dx \approx 0$$ (18)

where the unknown t is a function of x. The Euler-Lagrange equation is  

$$\frac{\partial F}{\partial \bar t} - \frac{d}{dx} \left[ \frac{\partial F}{\partial \bar t'}\right] = 0$$ (19)

To apply this equation I find  

$$\frac{\partial F}{\partial t}=2 \left[ p_x-\frac{\partial t}{\partial x}\right] \frac{\partial p_x}{\partial t}$$ (20)

and  

$$\frac{\partial F}{\partial t'}= - 2 \left[ p_x-\frac{\partial t}{\partial x}\right]$$ (21)

Substituting equations ( 20) and ( 21) into equation ( 19) and simplifying, I get:  

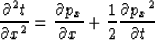$$\frac{\partial^2 t}{\partial x^2} = \frac{\partial p_x}{\partial x} + \frac{1}{2} \frac{\partial {p_x}^2}{\partial t}$$ (22)

It is straight forward to extend to the 3-D case.