Review of Basic Flattening Methodology

The basic idea is similar to phase unwrapping Claerbout (1999), but instead of summing phase differences to get total phase, dips are summed to get total time shifts that are then used to flatten the data. To apply the shifts, the central trace is held constant as a reference and all other traces are shifted vertically to match it.

The first step is to calculate dips everywhere in the 3-D seismic cube. Thus far only a simple dip estimation method has been used. Dip can be easily calculated using a plane-wave destructor as described in Claerbout (1992). For each point in the data cube two components of dip, p_x and p_y, are estimated in the x direction and y direction, respectively. These can be represented everywhere on the a mesh as vectors as 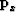${\bf p}_x$ and ${\bf p}_y$. 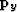For the dip in the x direction of a seismic cube with a wave field represented by u(x,y,t), I calculate the following locally:  

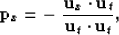$${\bf p}_x = - \ {{\bf u}_x \cdot {\bf u}_t \over {\bf u}_t \cdot {\bf u}_t},$$ (1)

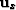where ${\bf u}_x$ is a vector with components 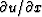$\partial u / \partial x$ taken on a mesh in (x,t) and 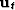${\bf u}_t$ is a vector with components 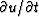$\partial u / \partial t$. Because I am calculating local dips, it is necessary to smooth the dips. I apply a triangle filter to both the numerator and denominator of equation (1). Since the dip estimation technique described in equation (1) is very dependent on the amplitude from trace-to-trace, amplitude variations along the horizons will create inaccuracies in dip estimation. This will, in turn, affect the quality of the flattening result. Therefore, an improved dip estimator will be very beneficial. For example, plane wave destructor filters Fomel (2001) will provide more robust dip information as they are less sensitive to aliasing and may require less smoothing than the dip estimation technique in equation (1).

The most basic flattening approach is to integrate dips on each time-slice in the data cube to get total time shifts (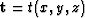${\bf t}=t(x,y,z)$). The gradient (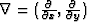$\nabla=( \frac{\partial }{\partial x}, \frac{\partial }{\partial y})$) of the time shifts can be related to the estimated dip (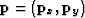${\bf p} = ({\bf p}_x,{\bf p}_y)$) in an overdetermined system with the following regression:

$${\bf \nabla t \quad = \quad \left[ \begin{array} {c} \frac{\... ...gin{array} {c}{\bf p}_x \\ \\ {\bf p}_y \end{array} \right] }.$$ (2)

The dips are summed to find a total time shift vector using:  

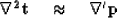$${\bf \nabla^2 t \quad \approx \quad \nabla' p}$$ (3)

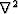where $\nabla^2$ is the Laplacian and 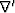$\nabla'$ is the divergence. Solving this equation for time-slices in both the Fourier domain and time-space domain is the basic flattening method described in the following sections.