Faults

To handle faults, I will have to leave the Fourier domain behind. The Fourier based method will estimate erroneous dips across faults. It will then try to honor these erroneous dips creating a result that behaves erratically. However, in the time-space domain, I should be able to handle all faults that have at least one half of the fault tip-line within the data cube. My approach is to create a masking operator (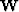$\bold W$) that will throw out dip estimates along faults. The method will try to remove all deformation except at the faults where it will allow complete slippage.

I want to find the time shifts, 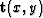${\bf t}(x,y)$, such that their gradient (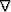$\bf \nabla$) is the dip, 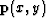${\bf p}(x,y)$. This sums across time-slices and is similar to equation (5). A time-space equivalent of equation (7) has also been implemented. I assume the dip, 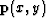${\bf p}(x,y)$, is not a function of the unknown 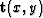${\bf t}(x,y)$ and write the fitting goal:

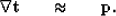$$\begin{eqnarray} \bf {\nabla t \quad }& \approx & \bf{ \quad p}.\end{eqnarray}$$ (8)

This is multiplied by the masking operator (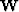$\bold W$) to throw out fitting equations at the faults as:

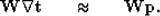$$\begin{eqnarray} \bf {W \nabla t \quad }& \approx & \bf{ \quad Wp}.\end{eqnarray}$$ (9)

The time shifts (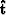$\bf \hat t$) can be found in a least-squares sense with:

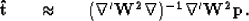$$\begin{eqnarray} \bf {\hat t \quad} & \approx & \bf{\quad (\nabla' W^2 \nabla )^{-1} \nabla' W^2 p}.\end{eqnarray}$$ (10)