




Next: Example 1: A simple
Up: Haines et al.: Multiple
Previous: Haines et al.: Multiple
The separation of a desired signal from unwanted noise can take many
forms, but is a central problem throughout exploration geophysics. Various
methods have been developed to address the issue, and we focus on
those applicable to cases where the signal and the noise can be
predicted with prediction error filters (PEF's) Abma (1995); Nemeth (1996); Soubaras (1994). In particular, we consider the
problem of multiples, and focus on their suppression in the angle domain.
We use the projection filtering method Abma (1995); Soubaras (1994) for this paper. Our goal is to efficiently compare the effects
of various model choices, so the small loss of
mathematical rigor pointed out by Guitton (2003b) is made up for
by the relative computational
stability. The projection filtering technique is described in detail
by Guitton (2003a). We review briefly:
We consider data (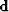 ) to be the sum of unknown signal (
) to be the sum of unknown signal ( ) and noise (
) and noise (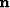 ):
):
| 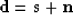 |
(1) |
and we estimate non-stationary PEF's 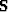 and
and 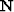 to be used as whitening
operators for the unknown signal and noise, respectively. The signal-noise
separation is based on the following fitting goals:
to be used as whitening
operators for the unknown signal and noise, respectively. The signal-noise
separation is based on the following fitting goals:
| 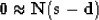 |
(2) |
and
| 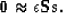 |
(3) |
A noise model is not explicitly estimated in the inversion. It is
considered to be the difference between the data and the estimated
signal (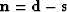 ).
).
The successful application of this method to a particular problem
requires careful choices of a number of different parameters and
inputs. These include the damping/weighting factor  and the dimensions
of the PEF's. A particularly important decision is the choice of models to be used for the
estimation of the PEF's
and the dimensions
of the PEF's. A particularly important decision is the choice of models to be used for the
estimation of the PEF's 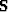 and
and 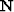 . Sava and Guitton (2003) use muting in the parabolic radon
transforms (PRT) domain to discriminate between multiples and primaries in
the angle domain, and we use their
results as a starting point for a PEF-based approach here. Rather
than simply subtracting the multiple
model output by the PRT approach from the original data, we use the primary and multiple models to estimate
PEF's which are then used in the signal/noise separation technique
outlined above. A series of synthetic and real data examples
illustrate the effectiveness of the technique, and enable us to test
various options for PEF estimation models.
. Sava and Guitton (2003) use muting in the parabolic radon
transforms (PRT) domain to discriminate between multiples and primaries in
the angle domain, and we use their
results as a starting point for a PEF-based approach here. Rather
than simply subtracting the multiple
model output by the PRT approach from the original data, we use the primary and multiple models to estimate
PEF's which are then used in the signal/noise separation technique
outlined above. A series of synthetic and real data examples
illustrate the effectiveness of the technique, and enable us to test
various options for PEF estimation models.





Next: Example 1: A simple
Up: Haines et al.: Multiple
Previous: Haines et al.: Multiple
Stanford Exploration Project
7/8/2003
![]() ) to be the sum of unknown signal (
) to be the sum of unknown signal (![]() ) and noise (
) and noise (![]() ):
):
![]() and the dimensions
of the PEF's. A particularly important decision is the choice of models to be used for the
estimation of the PEF's
and the dimensions
of the PEF's. A particularly important decision is the choice of models to be used for the
estimation of the PEF's ![]() and
and ![]() . Sava and Guitton (2003) use muting in the parabolic radon
transforms (PRT) domain to discriminate between multiples and primaries in
the angle domain, and we use their
results as a starting point for a PEF-based approach here. Rather
than simply subtracting the multiple
model output by the PRT approach from the original data, we use the primary and multiple models to estimate
PEF's which are then used in the signal/noise separation technique
outlined above. A series of synthetic and real data examples
illustrate the effectiveness of the technique, and enable us to test
various options for PEF estimation models.
. Sava and Guitton (2003) use muting in the parabolic radon
transforms (PRT) domain to discriminate between multiples and primaries in
the angle domain, and we use their
results as a starting point for a PEF-based approach here. Rather
than simply subtracting the multiple
model output by the PRT approach from the original data, we use the primary and multiple models to estimate
PEF's which are then used in the signal/noise separation technique
outlined above. A series of synthetic and real data examples
illustrate the effectiveness of the technique, and enable us to test
various options for PEF estimation models.