




Next: Example 2: A more
Up: Haines et al.: Multiple
Previous: Introduction
We begin with synthetic data for the simple one-dimensional case
described by Sava and Guitton (2003). Sava and Guitton (2003) use muting in the PRT domain to separate
input data (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a) into a primary model
(Figure
a) into a primary model
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c)
and a multiple model (Figure
c)
and a multiple model (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b). We are able to use this multiple model for
estimation of the noise PEF's, but find that the PRT-muted primary
model does not produce satisfactory results as a model for signal PEF estimation.
Because multiples and primaries overlap in some parts of the PRT
domain (most importantly at near offsets), the primary model still contains some multiple energy,
particularly in the deeper part of the record. We tested several
model options for estimating the signal PEF: the raw
PRT result;
b). We are able to use this multiple model for
estimation of the noise PEF's, but find that the PRT-muted primary
model does not produce satisfactory results as a model for signal PEF estimation.
Because multiples and primaries overlap in some parts of the PRT
domain (most importantly at near offsets), the primary model still contains some multiple energy,
particularly in the deeper part of the record. We tested several
model options for estimating the signal PEF: the raw
PRT result; 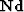 (the convolution of the noise PEF's with the original data
such that the signal is considered to be anything in the data that is
not removed by the noise PEF's); and a windowed version of the
PRT result. We know that
the lower part of the record contains no primary energy so we create a
signal model (Figure
(the convolution of the noise PEF's with the original data
such that the signal is considered to be anything in the data that is
not removed by the noise PEF's); and a windowed version of the
PRT result. We know that
the lower part of the record contains no primary energy so we create a
signal model (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d) by windowing and
zero-padding the PRT result. Using the windowed PRT result to
estimate our signal PEF, we can
remove nearly all of the multiple energy, leaving Figure
d) by windowing and
zero-padding the PRT result. Using the windowed PRT result to
estimate our signal PEF, we can
remove nearly all of the multiple energy, leaving Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) f as our final estimated signal.
CIG_syn_nice
f as our final estimated signal.
CIG_syn_nice
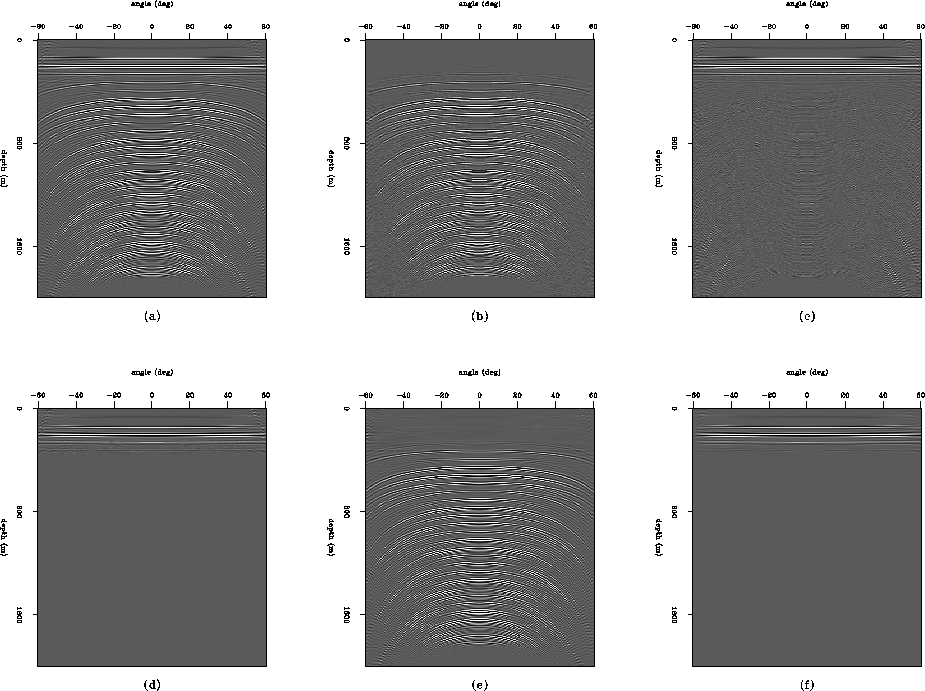
Figure 1 (a) Input data- a synthetic angle
gather. (b) Multiple model estimated with PRT approach. (c) Primary
model estimated from PRT approach. (d) Signal model used for PEF
estimation. (e) Multiple model estimated with PEF approach. (f)
Primary model estimated with PEF approach.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





While this result is clearly better than the PRT result, it is hardly
surprising given the simplicity of the situation and the choice of
signal model. It does, however, illustrate the important point that
with careful model choice we can cleanly separate primaries from
multiples in the angle domain, and encourages us to consider more
complicated cases. This example also illustrates an advantage of
PEF's over the PRT approach. The multiple model from the PRT
approach fails to capture some of the steeply dipping parts of the
multiple energy at the larger angles (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b), while this energy is captured by the PEF
approach (Figure
b), while this energy is captured by the PEF
approach (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) e). Although this energy
was not in the model used for noise PEF estimation, the same part of
the signal PEF estimation model contains only random noise, so the signal/noise
separation places that energy in the output noise model. The result
is a more thorough separation of signal from noise.
e). Although this energy
was not in the model used for noise PEF estimation, the same part of
the signal PEF estimation model contains only random noise, so the signal/noise
separation places that energy in the output noise model. The result
is a more thorough separation of signal from noise.





Next: Example 2: A more
Up: Haines et al.: Multiple
Previous: Introduction
Stanford Exploration Project
7/8/2003
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a) into a primary model
(Figure
a) into a primary model
(Figure