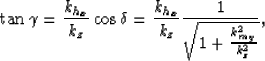Next: Application
Up: Tisserant and Biondi: 3-D
Previous: Definition of the 3-D
We first present the simplest extension to 3-D: the common-azimuth case.
In 2-D, the transformation from offset-gather to angle-gather
is accomplished by applying the relation Sava and Fomel (2000)
|  |
(1) |
where 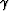 is the aperture angle, khx the in-line offset
wavenumber and kz the vertical wavenumber.
is the aperture angle, khx the in-line offset
wavenumber and kz the vertical wavenumber.
This relation can be applied in 3-D, but it is then assumed that
the two rays propagate vertically. In 3-D however, rays can propagate
out of the vertical plane. In the common-azimuth assumption, the two
rays propagate within a slanted plane. We call 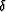 the dip angle
of the slanted propagation plane. The transformation from offset to
angle needs to take into account
the dip angle
of the slanted propagation plane. The transformation from offset to
angle needs to take into account 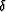 . The new form of equation
(1) is
. The new form of equation
(1) is
| 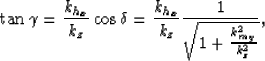 |
(2) |
where kmy is the cross-line midpoint wavenumber.
We give in Appendix A a geometrical and an analytical derivation
of equation (2). This equation is valid for common-azimuth
migration, that is to say, for an in-line orientation
of the source-receiver axis and for the coplanarity of the source and
receiver rays.





Next: Application
Up: Tisserant and Biondi: 3-D
Previous: Definition of the 3-D
Stanford Exploration Project
7/8/2003
![]() the dip angle
of the slanted propagation plane. The transformation from offset to
angle needs to take into account
the dip angle
of the slanted propagation plane. The transformation from offset to
angle needs to take into account ![]() . The new form of equation
(1) is
. The new form of equation
(1) is